题目内容
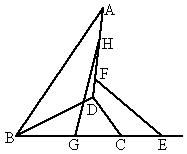
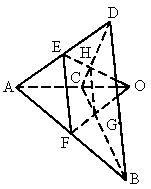
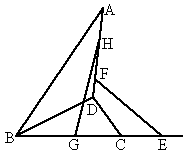
如图,
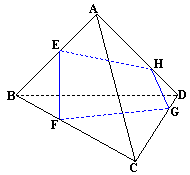
ABCD为空间四边形,点E,F分别是AB,BC的中点,点G,H分别在CD,AD上,且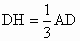 ,
,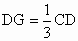 .求证:直线EH,FG必相交于一点,且这个交点在直线BD上.
.求证:直线EH,FG必相交于一点,且这个交点在直线BD上.
答案:
解析:
解析:
|
证明:如图所示,因为点 E,F分别是AB,BC的中点,从而可以得到EF∥AC.同理,因为点G,H分别在CD,AD上,且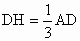 , , 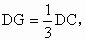 从而GH∥AC,故EF∥GH,从而直线EH,FG在同一平面上,又显然EH,FG不平行,故它们必交于一点. 从而GH∥AC,故EF∥GH,从而直线EH,FG在同一平面上,又显然EH,FG不平行,故它们必交于一点.
设直线 EH与BD直交于点O,过点D作平行于直线AB的辅助线DI,交EO于点I.从而可以得到△AEH∽△DIH,又EA=EB,从而有BE∥DI且BE=2DI,故得DO=BD.同样,设直线FG与BD相交于点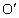 ,这点D作平行于直线BC的辅助线DJ,交FO于点J,利用相似三角形的性质也可以得到 ,这点D作平行于直线BC的辅助线DJ,交FO于点J,利用相似三角形的性质也可以得到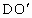 =BD,从而DO= =BD,从而DO=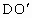 ,即点O与点 ,即点O与点 重合,故直线EH,BD,FG相交于同一点O. 重合,故直线EH,BD,FG相交于同一点O.
|

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目