题目内容
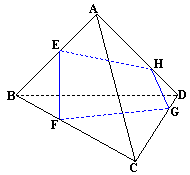
如图,ABCD为空间四边形,E、F分别为AD、AB的中点,G、H分别内分CB、CD成1∶2的点,求证:直线FC,EH,AC共点.
答案:略
解析:
解析:
|
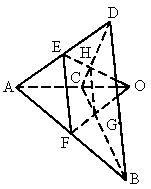
证明:连结 GH,由题意知,EF∥DB,且 . .
又∵  , ,
∴ HG∥BD,且 ,即 ,即 . .
∴ HG∥EF,且HG≠EF,∴EF与FG必相交,设EH∩FG=O.∵ O∈直线EH,∴O∈面ACD.又∵ O∈FC,∴O∈平面ACB,∴点 O在平面ACD和平面ACB的交线上,即O∈AC.∴直线 FG、EH、AC共点.根据公理 4,知EF∥HG,再确定EH与FG共面相交,由点、线、面的关系进行证明. |

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
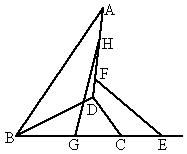
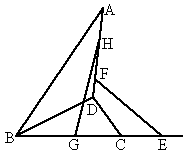

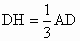 ,
,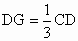 .求证:直线EH,FG必相交于一点,且这个交点在直线BD上.
.求证:直线EH,FG必相交于一点,且这个交点在直线BD上.