题目内容
（2012•宣城模拟）将6名年轻教师派送到4所初中支教，要求每所初中至少分得1名年轻教师，至多2名．则不同的派送方案种数为（ ）
分析：根据题意，分析可得4初中中，应有2所初中分得2名教师，剩余的2所各分得1名教师，分两步进行，首先将6名教师分为2-2-1-1的四组，由分组公式可得其分组方法数目，再将将四组对应4所初中，由排列公式计算可得其情况数目，进而由分步计数原理计算可得答案．
解答：解：根据题意，要求4所初中中每所初中至少分得1名年轻教师，至多2名，
则必须是其中2所初中分得2名教师，剩余的2所各分得1名教师，
可先将6名教师分为2-2-1-1的四组，有
=45种方法，
再将四组对应4所初中，有A44=24种方法，
则共有45×24=1080种派送方案；
故选B．
则必须是其中2所初中分得2名教师，剩余的2所各分得1名教师，
可先将6名教师分为2-2-1-1的四组，有
| ||||||||
| 2!×2! |
再将四组对应4所初中，有A44=24种方法，
则共有45×24=1080种派送方案；
故选B．
点评：本题考查排列、组合的应用，注意正确使用平均分组与不平均分组的公式．
练习册系列答案
阅读快车系列答案
相关题目
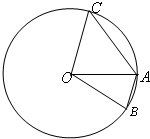（2012•宣城模拟）如图，⊙O的半径为1，点A，B，C是⊙O上的点，且∠AOB=30°，AC=2AB，则