题目内容
已知函数f(x)=mxm-n的导数为f′(x)=8x3,则mn= .
【答案】
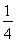
【解析】f′(x)=m(m-n)xm-n-1=8x3.
∴
解得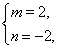
∴mn=2-2=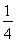 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
已知函数f(x)=mxm-n的导数为f′(x)=8x3,则mn= .
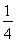
【解析】f′(x)=m(m-n)xm-n-1=8x3.
∴
解得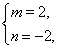
∴mn=2-2=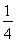 .
.

 阅读快车系列答案
阅读快车系列答案