Question

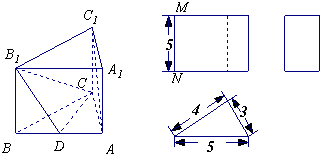已知三棱柱ABC-A₁B₁C₁的三视图如图所示，其中正视图和侧视图均为矩形，在俯视图的三角形中，三边长度分别为3，4，5．
（1）若正视图中MN=5，求三棱柱ABC-A₁B₁C₁的体积；
（2）在三棱柱ABC-A₁B₁C₁中，若D是底边的中点，求证：AC₁∥平面CDB₁．

Answer 1

分析：（Ⅰ）由题意可得该三棱柱是直三棱柱，底面△A₁B₁C₁为直角三角形，再根据棱柱的体积公式求得结果．
（Ⅱ）连接BC₁，交B₁C于O，再连接OD，则OD为△BAC₁的中位线，故有OD∥AC₁．再根据直线和平面平行的判定定理证得AC₁∥平面CDB₁．

解答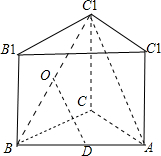：解：（Ⅰ）由于三棱柱的正视图和侧视图均为矩形，∴该三棱柱是直三棱柱，
在俯视图中，A₁C₁=3，B₁C₁=4，A₁B₁=5，∴A1C12+B1C12=A1B12，
∴△A₁B₁C₁为直角三角形，
∴V=

1

2

×3×4×5=30．
（Ⅱ）证明：在三棱柱ABC-A₁B₁C₁中，连接BC₁，交B₁C于O，
连接OD，由于D为AB的中点，则OD为△BAC₁的中位线，
∴OD∥AC₁．
∵AC₁?平面CDB₁，OD?平面CDB₁，
∴AC₁∥平面CDB₁．

点评：本题主要考查求棱柱的体积，直线和平面平行的判定定理的应用，属于中档题．