题目内容
【题目】给定无穷数列
，若无穷数列
满足：对任意
，都有
，则称与“接近”.
（1）设是首项为
，公比为的等比数列，
，，判断数列是否与接近，并说明理由；
（2）已知是公差为
的等差数列，若存在数列
满足：与接近，且在
这100个值中，至少有一半是正数，求的取值范围.
【答案】（1）数列
与
是接近的，详见解析（2）
【解析】
（1）写出与的通项公式，计算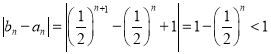
即可证明（2）由题意
，分公差
，公差
，
，公整
分类讨论，分别取满足条件
，利用
与接近的定义，计算
中所含的正数.
（1）数列与是接近的.理由如下：
因为是首项为
公比为的等比数列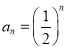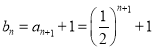，所以
，
，所以，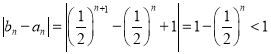
，
即数列与是接近的.
（2）因为是公差为
的等差数列，若存在数列满足：与是接近的，
可得，
①若公差，可取
，可得
，
则中有100个正数，符合题意；
②若公差，取
，则
，，
，
则中有100个正数，符合题意；
③若公差，可令
，
，
，
则
中有50个正数，符合题意；
④若公整，若存在数列满足：与是接近的，
即为
，
，
可得
，
则中无正数，不符合题意；
综上：的取值范围是.
练习册系列答案
相关题目
