题目内容
已知数集![]() 具有性质
具有性质![]() ;对任意的
;对任意的
![]() ,
,![]() 与
与![]() 两数中至少有一个属于
两数中至少有一个属于![]() 。
。
(Ⅰ)分别判断数集![]() 与
与![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(Ⅱ)证明:![]() ,且
,且![]() ;
;
(Ⅲ)证明:当![]() 时,
时,![]() 成等比数列。
成等比数列。
(Ⅰ)由于![]() 与
与![]() 均不属于数集
均不属于数集![]() ,∴该数集不具有性质P; 由于
,∴该数集不具有性质P; 由于![]() 都属于数集
都属于数集![]() ,∴该数集具有性质P。
,∴该数集具有性质P。
(Ⅱ)证明见解析。
(Ⅲ)证明见解析。
解析:
本题主要考查集合、等比数列的性质,考查运算能力、推理论证能力、分
分类讨论等数学思想方法。本题是数列与不等式的综合题,属于较难层次题。
(Ⅰ)由于![]() 与
与![]() 均不属于数集
均不属于数集![]() ,∴该数集不具有性质P;由于
,∴该数集不具有性质P;由于![]() 都属于数集
都属于数集![]() , ∴该数集具有性质P。
, ∴该数集具有性质P。
(Ⅱ)∵![]() 具有性质P,∴
具有性质P,∴![]() 与
与![]() 中至少有一个属于A,
中至少有一个属于A,
由于![]() ,∴
,∴![]() ,故
,故![]() 。
。
从而![]() ,∴
,∴![]() 。
。
∵![]() , ∴
, ∴![]() ,故
,故![]() 。
。
由A具有性质P可知![]() 。
。
又∵![]() ,
,
∴![]() ,
,
从而![]() ,
,
∴![]() 。
。
(Ⅲ)由(Ⅱ)知,当![]() 时,有
时,有![]() ,即
,即![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
由A具有性质P可知![]() 。
。
由![]() ,得
,得![]() ,且
,且![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() 是首项为1,公比为
是首项为1,公比为![]() 成等比数列。
成等比数列。

练习册系列答案
相关题目
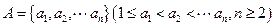 具有性质
具有性质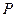 ;对任意的
;对任意的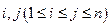 ,
,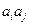 与
与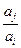 两数中至少有一个属于
两数中至少有一个属于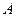 。
。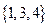 与
与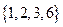 是否具有性质
是否具有性质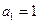 ,且
,且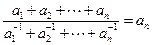 ;
;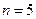 时,
时,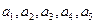 成等比数列。
成等比数列。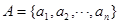 ,其中
,其中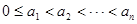 ,且
,且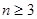 ,若对
,若对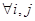 (
(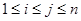 ),
),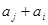 与
与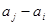 两数中至少有一个属于
两数中至少有一个属于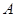 ,则称数集
,则称数集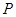 .
.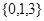 与数集
与数集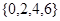 是否具有性质
是否具有性质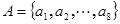 具有性质
具有性质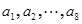 是否为等差数列,若是等差数列,请证明;若不是,请说明理由.
是否为等差数列,若是等差数列,请证明;若不是,请说明理由.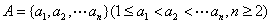 具有性质
具有性质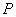 ;对任意的
;对任意的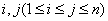 ,
,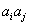 与
与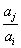 两数中至少有一个属于
两数中至少有一个属于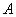 。
。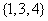 与
与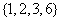 是否具有性质
是否具有性质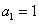 ,且
,且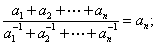
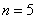 时,
时,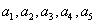 成等比数列。
成等比数列。