题目内容
已知数集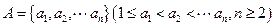 具有性质
具有性质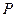 ;对任意的
;对任意的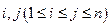 ,
,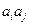 与
与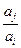 两数中至少有一个属于
两数中至少有一个属于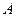 。
。
(Ⅰ)分别判断数集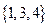 与
与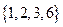 是否具有性质
是否具有性质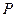 ,并说明理由;
,并说明理由;
(Ⅱ)证明: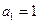 ,且
,且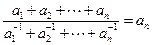 ;
;
(Ⅲ)证明:当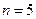 时,
时,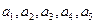 成等比数列。
成等比数列。
(Ⅰ)由于 与
与 均不属于数集
均不属于数集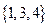 ,∴该数集不具有性质P;由于
,∴该数集不具有性质P;由于 都属于数集
都属于数集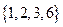 ,∴该数集具有性质P。
,∴该数集具有性质P。
(Ⅱ)证明见解析。
(Ⅲ)证明见解析。
解析

练习册系列答案
相关题目
题目内容
已知数集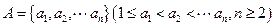 具有性质
具有性质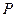 ;对任意的
;对任意的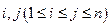 ,
,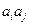 与
与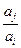 两数中至少有一个属于
两数中至少有一个属于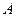 。
。
(Ⅰ)分别判断数集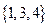 与
与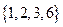 是否具有性质
是否具有性质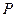 ,并说明理由;
,并说明理由;
(Ⅱ)证明: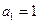 ,且
,且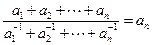 ;
;
(Ⅲ)证明:当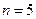 时,
时,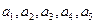 成等比数列。
成等比数列。
(Ⅰ)由于 与
与 均不属于数集
均不属于数集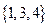 ,∴该数集不具有性质P;由于
,∴该数集不具有性质P;由于 都属于数集
都属于数集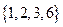 ,∴该数集具有性质P。
,∴该数集具有性质P。
(Ⅱ)证明见解析。
(Ⅲ)证明见解析。
解析
