Question

在正四面体ABCD中,E为棱AD中点,连结CE,求CE和平面BCD所成角的正弦值.

Answer 1

解析:如图,设点A在平面BCD内的射影为O,∵ABCD为正四面体,

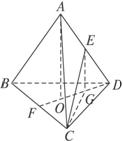
∴O为△BCD的中心,连结DO交BC于F,过E点作EG⊥DF于G,连结CG.

∵在平面AOD中,AO⊥DO、EG⊥DO,

∴AO∥EG.又∵AO⊥平面BCD,

∴EG⊥平面BCD,即∠ECG为CE与平面BCD所成的角.

令正四面体的棱长为1,可求得CE=,OD=,

∴AO=.而EG=AO=,

∴在Rt△ECG中,sin∠ECG==.