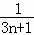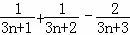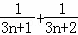题目内容
已知向量m=(-1,cosωx+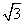 sinωx),n=(f(x),cosωx),其中ω>0,且m⊥n,又函数f(x)的图象任意两相邻对称轴间距为
sinωx),n=(f(x),cosωx),其中ω>0,且m⊥n,又函数f(x)的图象任意两相邻对称轴间距为 π.
π.
(1)求ω的值;
(2)设α是第一象限角,且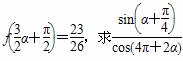 的值.
的值.
(1)由题意得m·n=0,所以,
f(x)=cosωx·(cosωx+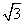 sinωx)
sinωx)
= +
+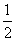 ,
,
根据题意知,函数f(x)的最小正周期为3π.
又ω>0,所以ω= .
.
(2)由(1)知f(x)=
所以
=cosα+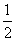 =
= ,
,
解得cosα= ,
,
因为α是第一象限角,故sinα= ,
,
所以, =
= ·
· =-
=-
.

练习册系列答案
相关题目
设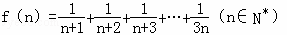 ,则f(n+1)﹣f(n)=( )
,则f(n+1)﹣f(n)=( )
|
| A. |
| B. |
|
|
| C. |
| D. |
|
 ,α∈(-
,α∈(-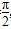 ,0),则tanα=________.
,0),则tanα=________. ),且cosα=
),且cosα= x,则sin(α+
x,则sin(α+ )=________
)=________ ),则sinx=( )
),则sinx=( ) B.
B. 
 D.
D. 

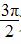 )(x∈R),下面结论错误的是( )
)(x∈R),下面结论错误的是( )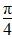 对称
对称 ]上是增函数
]上是增函数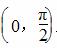 ,x2>x1,y1=
,x2>x1,y1= ,y2=
,y2=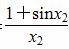 ,则( )
,则( )