题目内容
观察下列等式:
 +2=4;
+2=4; ×2=4;
×2=4; +3=
+3= ;
; ×3=
×3= ;
; +4=
+4= ;
; ×4=
×4= ;…,根据这些等式反映的结果,可以得出一个关于自然数n的等式,这个等式可以表示为______________________.
;…,根据这些等式反映的结果,可以得出一个关于自然数n的等式,这个等式可以表示为______________________.
 +2=4;
+2=4; ×2=4;
×2=4; +3=
+3= ;
; ×3=
×3= ;
; +4=
+4= ;
; ×4=
×4= ;…,根据这些等式反映的结果,可以得出一个关于自然数n的等式,这个等式可以表示为______________________.
;…,根据这些等式反映的结果,可以得出一个关于自然数n的等式,这个等式可以表示为______________________. +(n+1)=
+(n+1)= ×(n+1)(n∈N*)
×(n+1)(n∈N*)由归纳推理得 +(n+1)=
+(n+1)= =
= ,
, ×(n+1)=
×(n+1)= ,所以得出结论
,所以得出结论 +(n+1)=
+(n+1)= ×(n+1)(n∈N*).
×(n+1)(n∈N*).
 +(n+1)=
+(n+1)= =
= ,
, ×(n+1)=
×(n+1)= ,所以得出结论
,所以得出结论 +(n+1)=
+(n+1)= ×(n+1)(n∈N*).
×(n+1)(n∈N*).
练习册系列答案
相关题目
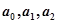 成等差数列时,有
成等差数列时,有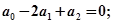 当
当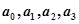 成等差数列时,有
成等差数列时,有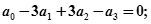 当
当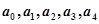
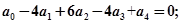 成等差数列时,有由此归纳,当
成等差数列时,有由此归纳,当 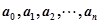 成等差数列时,有
成等差数列时,有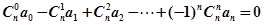 .如果
.如果 ,其中
,其中 表示不小于
表示不小于 的最小整数,如
的最小整数,如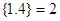 ,
,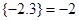 .当
.当 (
( )时,函数
)时,函数 的值域为
的值域为 ,记集合
,记集合 ,则
,则 ________________.
________________. ,
, ,
, ,……,
,……, .以上运用的是什么形式的推理?__ __ .
.以上运用的是什么形式的推理?__ __ .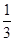 ”.拓展到空间,类比平面几何的上述结论,则正四面体的内切球半径等于这个正四面体的高的________ .
”.拓展到空间,类比平面几何的上述结论,则正四面体的内切球半径等于这个正四面体的高的________ .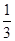 [k(k+1)(k+2)-(k-1)k(k+1)],
[k(k+1)(k+2)-(k-1)k(k+1)],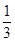 +
+ =1;
=1;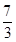 +
+ +
+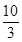 +
+ =12;
=12;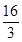 +
+ +
+ +
+ +
+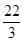 +
+ =39;
=39; +
+ +
+ +
+ +…+
+…+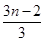 +
+ =________(最后结果用m,n表示).
=________(最后结果用m,n表示). 则ak+1=( ).
则ak+1=( ).
 -
-