题目内容
已知椭圆C:![]() (
(![]() ),其离心率为
),其离心率为![]() ,两准线之间的距离为
,两准线之间的距离为![]() 。(1)求
。(1)求![]() 之值;(2)设点A坐标为(6, 0),B为椭圆C上的动点,以A为直角顶点,作等腰直角△ABP(字母A,B,P按顺时针方向排列),求P点的轨迹方程。
之值;(2)设点A坐标为(6, 0),B为椭圆C上的动点,以A为直角顶点,作等腰直角△ABP(字母A,B,P按顺时针方向排列),求P点的轨迹方程。
(1)a=5,b=3(2)![]()
解析:
(1)设c为椭圆的焦半径,则
![]() 。
。
于是有a=5,b=3。
(2) 解法一:设B点坐标为![]() ,P点坐标为
,P点坐标为![]() 。于是有
。于是有
![]()
因为![]() ,所以有
,所以有
![]() 。 (A1 )
。 (A1 )
又因为ABP为等腰直角三角形,所以有 AB=AP,即
![]() 。 (A2 )
。 (A2 )
由(A1)推出![]() ,代入(A2),得
,代入(A2),得
![]()
从而有 ![]() ,即
,即![]() (不合题意,舍去)或
(不合题意,舍去)或![]() 。
。
代入椭圆方程,即得动点P的轨迹方程
![]()
解法二: 设![]() ,
,![]() ,则以A为圆心,r为半径的圆的参数方程为
,则以A为圆心,r为半径的圆的参数方程为
![]() 。
。
设AB与x轴正方向夹角为![]() ,B点的参数表示为
,B点的参数表示为
 ,
,
P点的参数表示为
 .
.
从上面两式,得到
 。
。
又由于B点在椭圆上,可得
![]() 。
。
此即为P点的轨迹方程。

练习册系列答案
相关题目
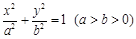 ,其离心率为
,其离心率为 ,经过椭圆焦点且垂直于长轴的弦长为3.
,经过椭圆焦点且垂直于长轴的弦长为3. 与椭圆C交于A、B两点,P为椭圆上的点,O为坐标原点,且满足
与椭圆C交于A、B两点,P为椭圆上的点,O为坐标原点,且满足 ,求
,求 的取值范围.
的取值范围. ,F
,F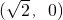 为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2.
为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2. ,F
,F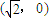 为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2.
为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2.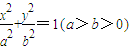 ,F
,F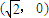 为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2.
为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2.