题目内容
已知椭圆C: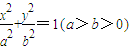 ,F
,F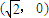 为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2.
为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2.(1)求椭圆C的方程;
(2)直线l:y=kx+m(km≠0)与椭圆C交于A、B两点,若线段AB中点在直线x+2y=0上,求△FAB的面积的最大值.
【答案】分析:(1)利用F 为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2,建立方程组,求得几何量,即可求得椭圆方程;
为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2,建立方程组,求得几何量,即可求得椭圆方程;
(2)直线l:y=kx+m(km≠0)与椭圆联立,利用线段AB中点在直线x+2y=0上求得k的值,求出|AB|,及点F 到直线AB的距离
到直线AB的距离 ,表示出三角形的面积,利用求导数的方法,即可确定△FAB的面积的最大值.
,表示出三角形的面积,利用求导数的方法,即可确定△FAB的面积的最大值.
解答:解:(1)由题意 ,解得
,解得 ,∴所求椭圆方程为
,∴所求椭圆方程为 . …(4分)
. …(4分)
(2)直线l:y=kx+m(km≠0)与椭圆联立,消去y得(1+2k2)x2+4kmx+2m2-4=0,…(5分)
△=16k2m2-4(1+2k2)(2m2-4)=8(6-m2)>0,∴
设A(x1,y1),B(x2,y2)P(x,y),由韦达定理得 =
= ,
, .
.
由点P在直线x+2y=0上,得k=1. …(7分)
所以|AB|= =
= .
.
又点F 到直线AB的距离
到直线AB的距离 .
.
∴△FAB的面积为 =
= (|m|<
(|m|< ,m≠0).…(10分)
,m≠0).…(10分)
设u(m)=(6-m2)(m+ )2(|m|<
)2(|m|< ,m≠0),则令u′(m)=-2(2m+3
,m≠0),则令u′(m)=-2(2m+3 )(m+
)(m+ )(m-
)(m- )=0,可得m=-
)=0,可得m=- 或m=-
或m=- 或m=
或m= ;
;
当 时,u′(m)>0;当
时,u′(m)>0;当 时,u′(m)<0;
时,u′(m)<0;
当 时,u′(m)>0;当
时,u′(m)>0;当 时,u′(m)<0
时,u′(m)<0
又u( )=
)= ,
,
所以当m= 时,△FAB的面积取最大值
时,△FAB的面积取最大值 …(12分)
…(12分)
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查三角形面积的计算,考查利用导数的方法求函数的最值,属于中档题.
 为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2,建立方程组,求得几何量,即可求得椭圆方程;
为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2,建立方程组,求得几何量,即可求得椭圆方程;(2)直线l:y=kx+m(km≠0)与椭圆联立,利用线段AB中点在直线x+2y=0上求得k的值,求出|AB|,及点F
 到直线AB的距离
到直线AB的距离 ,表示出三角形的面积,利用求导数的方法,即可确定△FAB的面积的最大值.
,表示出三角形的面积,利用求导数的方法,即可确定△FAB的面积的最大值.解答:解:(1)由题意
 ,解得
,解得 ,∴所求椭圆方程为
,∴所求椭圆方程为 . …(4分)
. …(4分)(2)直线l:y=kx+m(km≠0)与椭圆联立,消去y得(1+2k2)x2+4kmx+2m2-4=0,…(5分)
△=16k2m2-4(1+2k2)(2m2-4)=8(6-m2)>0,∴

设A(x1,y1),B(x2,y2)P(x,y),由韦达定理得
 =
= ,
, .
.由点P在直线x+2y=0上,得k=1. …(7分)
所以|AB|=
 =
= .
.又点F
 到直线AB的距离
到直线AB的距离 .
.∴△FAB的面积为
 =
= (|m|<
(|m|< ,m≠0).…(10分)
,m≠0).…(10分)设u(m)=(6-m2)(m+
 )2(|m|<
)2(|m|< ,m≠0),则令u′(m)=-2(2m+3
,m≠0),则令u′(m)=-2(2m+3 )(m+
)(m+ )(m-
)(m- )=0,可得m=-
)=0,可得m=- 或m=-
或m=- 或m=
或m= ;
;当
 时,u′(m)>0;当
时,u′(m)>0;当 时,u′(m)<0;
时,u′(m)<0;当
 时,u′(m)>0;当
时,u′(m)>0;当 时,u′(m)<0
时,u′(m)<0又u(
 )=
)= ,
,
所以当m=
 时,△FAB的面积取最大值
时,△FAB的面积取最大值 …(12分)
…(12分)点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查三角形面积的计算,考查利用导数的方法求函数的最值,属于中档题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 ,F
,F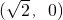 为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2.
为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2. ,F
,F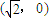 为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2.
为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2. ,F为其右焦点,A为左顶点,l为右准线,过F的直线l′与椭圆交于异于A点的P、Q两点.
,F为其右焦点,A为左顶点,l为右准线,过F的直线l′与椭圆交于异于A点的P、Q两点. 的取值范围;
的取值范围;
 ,F为其右焦点,A为左顶点,l为右准线,过F的直线l′与椭圆交于异于A点的P、Q两点.
,F为其右焦点,A为左顶点,l为右准线,过F的直线l′与椭圆交于异于A点的P、Q两点. 的取值范围;
的取值范围;