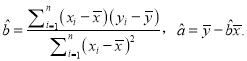题目内容
【题目】如甲图所示,在矩形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点,将
的中点,将![]() 沿
沿![]() 折起到
折起到![]() 位置,使平面
位置,使平面![]() 平面
平面![]() ,得到乙图所示的四棱锥
,得到乙图所示的四棱锥![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
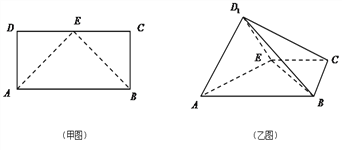
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)取![]() 中点
中点![]() ,连
,连![]() ,证得
,证得![]() ,又
,又![]() 平面
平面![]() 平面
平面![]() ,证得
,证得![]() 平面
平面![]() ,证明
,证明![]() 再利用线面的判定定理,即可证得
再利用线面的判定定理,即可证得![]() 平面
平面![]()
(Ⅱ)由题意,取![]() 中点
中点![]() ,以
,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
, ![]() 为
为![]() 轴正方向建立空间直角坐标系
轴正方向建立空间直角坐标系![]() ,由(Ⅰ)知:
,由(Ⅰ)知: ![]() 是平面
是平面![]() 的法向量,设平面
的法向量,设平面![]() 的法向量为
的法向量为![]() ,利用空间向量的夹角公式,即可求解结论.
,利用空间向量的夹角公式,即可求解结论.
试题解析:
(Ⅰ)如下图,取![]() 中点
中点![]() ,连
,连![]() ,在
,在![]() 中,
中, ![]() ,
, ![]() ,又
,又![]() 平面
平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,即
,即![]() .在
.在![]() 中,易得
中,易得![]() ,
, ![]() ,
, ![]() ,
,
![]() ,又
,又![]() ,
,
![]() 平面
平面![]()

(Ⅱ)由题意,取![]() 中点
中点![]() ,以
,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() ,
, ![]() 为
为![]() 轴正方向建立间直角坐标系
轴正方向建立间直角坐标系![]() 如图所示,则
如图所示,则![]() ,由(Ⅰ)知:
,由(Ⅰ)知: ![]() 是平面
是平面![]() 的法向量,设平面
的法向量,设平面![]() 的法向量为
的法向量为![]() ,则
,则
 ,令
,令![]() ,则
,则![]() ,
, ![]() ,
,
![]() ,设二面角
,设二面角![]() 的平面角为
的平面角为![]() ,
,
则![]()

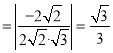 ,
,
由图可知,二面角![]() 的平面角为钝角,
的平面角为钝角,
![]() ,即:二面角
,即:二面角![]() 的余弦值为
的余弦值为![]()

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
【题目】某企业为了对生产的一种新产品进行合理定价,将该产品按事先拟定的价格进行试销,得到以下数据:
单价x(元/件) | 60 | 62 | 64 | 66 | 68 | 70 |
销量y(件) | 91 | 84 | 81 | 75 | 70 | 67 |
(I)画出散点图,并求![]() 关于
关于![]() 的回归方程;
的回归方程;
(II)已知该产品的成本是36元/件,预计在今后的销售中,销量与单价仍然服从(I)中的关系,为使企业获得最大利润,该产品的单价应定为多少元(精确到元)?
附:回归直线![]() 的斜率和截距的最小二乘法估计公式分别为:
的斜率和截距的最小二乘法估计公式分别为: