题目内容
已知数列 的前n项和为
的前n项和为 ,且
,且 ,(n=1,2,3…)数列
,(n=1,2,3…)数列 中,
中, ,点
,点 在直线
在直线 上。
上。
(Ⅰ)求数列 和
和 的通项公式;
的通项公式;
(Ⅱ)记 ,求满足
,求满足 的最大正整数n。
的最大正整数n。
 的前n项和为
的前n项和为 ,且
,且 ,(n=1,2,3…)数列
,(n=1,2,3…)数列 中,
中, ,点
,点 在直线
在直线 上。
上。(Ⅰ)求数列
 和
和 的通项公式;
的通项公式;(Ⅱ)记
 ,求满足
,求满足 的最大正整数n。
的最大正整数n。解:(I)∵ 
∴ 当 时,
时,
即 ∵
∵  ∴
∴ 

即数列 是等比数列.
是等比数列.
∵ ∴
∴  即
即
∴ …………………3分
…………………3分
∵ 点 在直线
在直线 上
上
∴ ∴
∴ 
即数列 是等差数列,又
是等差数列,又 ∴
∴  …………………6分
…………………6分
(II)
 ①(7分)
①(7分)
∴ ②
②
①-②得
即 …………………9分
…………………9分
∴ (10分)
(10分)
∵ 即
即
于是 (11分)
(11分)
又由于当 时,
时, (12分)
(12分)
当 时,
时, (13分)
(13分)
故满足条件 最大的正整数n为4
最大的正整数n为4

∴ 当
 时,
时,
即
 ∵
∵  ∴
∴ 

即数列
 是等比数列.
是等比数列. ∵
 ∴
∴  即
即
∴
 …………………3分
…………………3分∵ 点
 在直线
在直线 上
上∴
 ∴
∴ 
即数列
 是等差数列,又
是等差数列,又 ∴
∴  …………………6分
…………………6分(II)

 ①(7分)
①(7分)∴
 ②
②①-②得

即
 …………………9分
…………………9分∴
 (10分)
(10分)∵
 即
即
于是
 (11分)
(11分)又由于当
 时,
时, (12分)
(12分)当
 时,
时, (13分)
(13分)故满足条件
 最大的正整数n为4
最大的正整数n为4略

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
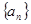 的前
的前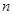 项和为
项和为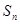 ,
,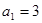 ,若数列
,若数列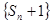 是公比为
是公比为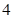 的等比数列.
的等比数列. 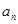 ;
;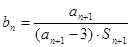 ,
,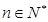 ,求数列
,求数列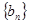 的前
的前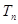 .
.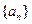 是递增数列,且满足
是递增数列,且满足 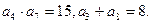
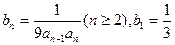 ,求数列
,求数列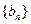 的前
的前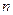 项和
项和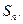
 n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
n∈N*, Sn,Sn+1,Sn+2不构成等比数列.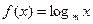 (m为常数,m>0且
(m为常数,m>0且 )
) 是首项为4,公差为2的等差数列.
是首项为4,公差为2的等差数列.  是等比数列;
是等比数列; ,且数列{bn}的前n项和
,且数列{bn}的前n项和 ,当
,当 时,求
时,求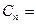
 ,问是否存在
,问是否存在 ,使得
,使得 中每一项恒小于它后面的项?
中每一项恒小于它后面的项? 其中
其中 为预测期内年增长率,
为预测期内年增长率,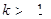 ,
, 为预测期人口数,
为预测期人口数, 为初期人口数,
为初期人口数,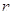 为预测期间隔年数。如果在某一时期有
为预测期间隔年数。如果在某一时期有 ,那么在这期间人口数
,那么在这期间人口数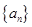 中,
中,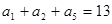 ,且
,且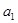 、
、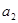 、
、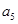 成等比数列,则数列
成等比数列,则数列 ,若
,若 成等差数列(公差不为零),则
成等差数列(公差不为零),则
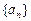 中,
中, 前5项和
前5项和 则其公差
则其公差