题目内容
(本题满分6分)已知函数 且此函数图象过点(1,5).
且此函数图象过点(1,5).
(1)求实数m的值;
(2)判断 在
在 上的单调性,并证明你的结论。
上的单调性,并证明你的结论。
(1) (2)用导数证明或用定义证明.
(2)用导数证明或用定义证明.
【解析】
试题分析:(1)代入(1,5)即可求解;(2)用导数证明或用定义证明.
解题思路:证明函数的单调性,主要方法有导数法和定义法,现在教学倾向于导数法.
试题解析:(1)代入 ,得
,得 ,解得
,解得 ;
;
(2)由(1),得 ,则
,则 ;当
;当 时,
时, 且不恒为0,所以
且不恒为0,所以 在
在 单调递增.
单调递增.
考点:1.待定系数法;2.利用导数研究函数的单调性.
考点分析: 考点1:函数的单调性 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
某校为了研究学生的性别和对待某一活动的态度(支持和不支持两种态度)的关系,运用2×2列联表进行独立性检验,经计算K2=7.069,则最高有 (填百分数)的把握认为“学生性别与是否支持该活动有关系”.
附:
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
某工厂生产某种产品的产量x(吨)与相应的生产能耗y(吨标准煤)有如下几组样本数据:
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
据相关性检验,这组样本数据具有线性相关关系,通过线性回归分析,求得其回归直线的斜率为0.7,则这组样本数据的回归直线方程是
A. =0.7x+0.35 B.
=0.7x+0.35 B. =0.7x+1
=0.7x+1
C. =0.7x+2.05 D.
=0.7x+2.05 D. =0.7x+0.45
=0.7x+0.45
 ,则
,则 B.若
B.若 ,则
,则
 ,则
,则 D.若
D.若 ,则
,则

 的左、右焦点分别为F1、F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为( ).
的左、右焦点分别为F1、F2,P是C上的点,PF2⊥F1F2,∠PF1F2=30°,则C的离心率为( ). B.
B. C.
C. D.
D.
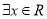 ,使得
,使得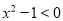 ”的否定是“
”的否定是“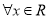 ,均有
,均有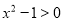 ”;
”;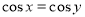 ,则x=y”的逆否命题是真命题:
,则x=y”的逆否命题是真命题: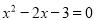 ”的否命题是“若
”的否命题是“若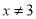 ,则
,则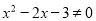 ”;
”;  的左顶点A的斜率为
的左顶点A的斜率为 的直线交椭圆
的直线交椭圆 于另一个点
于另一个点 ,且点
,且点 轴上的射影恰好为右焦点
轴上的射影恰好为右焦点 ,若
,若 则椭圆离心率的取值范围是( )
则椭圆离心率的取值范围是( )
 B.
B. C.
C. D.
D.
 与双曲线C2的公共焦点,A、B分别是C1与C2在第二、四象限的公共点。若四边形AF1BF2为矩形,则C2的离心率是( )
与双曲线C2的公共焦点,A、B分别是C1与C2在第二、四象限的公共点。若四边形AF1BF2为矩形,则C2的离心率是( )
 B.
B. C.
C. D.
D.