Question

（2013•红桥区二模）一海轮在B处望见A处的小岛，测得小岛在海轮北偏东75°，海轮由B处向正东方向行驶8n mile到达C处，测得此时小岛在海轮北偏东60°．这艘海轮不改变方向继续前行，则海轮与小岛的最近距离为

4 nmile

．

Answer 1

分析：如图所示：由题意可得，BC=8，∠ABC=15°，∠ACB=90°+60°=150°，可得∠BAC=15°，从而得到△ABC为等腰△ABC中，可得AC的值，直角△ACD中，再根据直角三角形中
的边角关系求得海轮与小岛的最近距离为AD 的值．

解答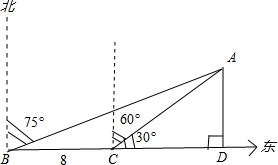：解：如图所示：由题意可得，BC=8，∠ABC=15°，∠ACB=90°+60°=150°，∴∠BAC=15°．
故△ABC为等腰三角形，∴BC=AC=8．
直角三角形ACD中，由于∠ACD=30°，∴AD=

1

2

AC=4，即海轮与小岛的最近距离为AD=4 （nmile ），
故答案为 4 （nmile）．

点评：本题主要考查三角形内角和公式的应用，直角三角形中的边角关系，体现了数形结合的数学思想，属于中档题．