题目内容
已知向量
，其中a、b、c分别是
的三内角A、B、C的对边长.
（1）求
的值；
（2）求
的最大值.
，其中a、b、c分别是的三内角A、B、C的对边长.（1）求
的值；（2）求
的最大值.（1）
（2）
（2）本试题主要是考查了解三角形的运用。
（1）利用正弦定理，结合向量的数量积公式得到结论。
（2）利用正切值相等，结合两角和差的正切公式得到求解。
（1）利用正弦定理，结合向量的数量积公式得到结论。
（2）利用正切值相等，结合两角和差的正切公式得到求解。
练习册系列答案
相关题目
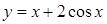在区间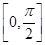
上的最大值是 ．
，
，
，
的最大值及
的取值范围；
的最值.
在一个周期内的图象如图所示.则
的图象可由函数y=cosx的图象（纵坐标不变） （ ）
倍,再向左平移
个单位
倍，再向右平移
个单位
个单位
个单位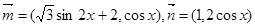
，设函数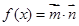
.
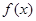的最小正周期与单调递减区间；
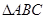中，
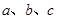分别是角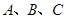
的对边，若
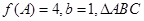的面积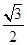
，求a的值. 
,
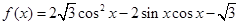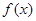的单调递增区间.
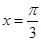处的切线方程. 
．
的最小正周期；
个单位，得到函数
的图象，求函数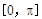
上的最大值和最小值．
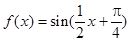，求函数在区间
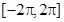上的单调增区间；
.
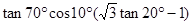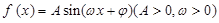的图象如图所示，则
．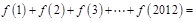