题目内容
已知∠ACB=90°,S为平面ABC外一点,且∠SCA=∠SCB=60°,则直线SC和平面ABC所成的角为
45°
45°
.分析:过S作SO⊥平面ABC,垂足为O,则O在∠ACB的平分线上,且∠SCO为直线SC和平面ABC所成的角,利用∠ACB=90°,∠SCA=∠SCB=60°,即可求得结论.
解答: 解:过S作SO⊥平面ABC,垂足为O,则O在∠ACB的平分线上,且∠SCO为直线SC和平面ABC所成的角.
解:过S作SO⊥平面ABC,垂足为O,则O在∠ACB的平分线上,且∠SCO为直线SC和平面ABC所成的角.
过O作OD⊥CB,连接SD,则SD⊥CB
设SC=a,则在△SCD中,∠SCD=60°,∴CD=
在△COD中,∠OCD=45°,∴CO=
在△SCO中,cos∠SCO=
=
∴∠SCO=45°
故答案为:45°
 解:过S作SO⊥平面ABC,垂足为O,则O在∠ACB的平分线上,且∠SCO为直线SC和平面ABC所成的角.
解:过S作SO⊥平面ABC,垂足为O,则O在∠ACB的平分线上,且∠SCO为直线SC和平面ABC所成的角.过O作OD⊥CB,连接SD,则SD⊥CB
设SC=a,则在△SCD中,∠SCD=60°,∴CD=
| a |
| 2 |
在△COD中,∠OCD=45°,∴CO=
| ||
| 2 |
在△SCO中,cos∠SCO=
| CO |
| SC |
| ||
| 2 |
∴∠SCO=45°
故答案为:45°
点评:本题考查线面角,解题的关键是正确作出线面角,属于中档题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
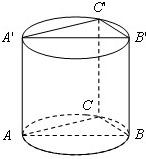 如图,直三棱柱ABC-A′B′C′内接于高为
如图,直三棱柱ABC-A′B′C′内接于高为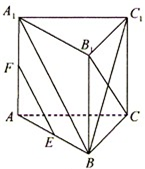 如图,在直三棱柱ABC-A1B1C1中,已知∠ACB=90°,BC=CC1,E、F分别为AB、AA1的中点.
如图,在直三棱柱ABC-A1B1C1中,已知∠ACB=90°,BC=CC1,E、F分别为AB、AA1的中点. (2012•江苏三模)如图,在直三棱柱ABC-A1B1C1中,已知∠ACB=90°,M为A1B与AB1的交点,N为棱B1C1的中点.
(2012•江苏三模)如图,在直三棱柱ABC-A1B1C1中,已知∠ACB=90°,M为A1B与AB1的交点,N为棱B1C1的中点. (2009•红桥区二模)如图是一圆锥的正视图,已知∠ACB=90°,AC=BC=
(2009•红桥区二模)如图是一圆锥的正视图,已知∠ACB=90°,AC=BC=