题目内容
直线y=a与函数 =x3-3x的图象有相异的三个公共点,则a的取值范围是 _____.
=x3-3x的图象有相异的三个公共点,则a的取值范围是 _____.
 =x3-3x的图象有相异的三个公共点,则a的取值范围是 _____.
=x3-3x的图象有相异的三个公共点,则a的取值范围是 _____.(-2,2)
试题分析:结合函数图象,a介于f(x)的极大值和极小值之间。
因为,
 =x3-3x ,所以,f’(x)=3x²-3,令f'(x)=0,得:x=-1,x=1
=x3-3x ,所以,f’(x)=3x²-3,令f'(x)=0,得:x=-1,x=1f(-1)=2,f(1)=-2
所以,-2<a<2,故答案为(-2,2)。
点评:简单题,利用数形结合法,将问题转化成利用导数研究函数的极值。

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 , 四个函数中,当
, 四个函数中,当 时, 满足不等式
时, 满足不等式 的是
的是



 ,函数
,函数 ,
, .(
.( 的图象连续不断)
的图象连续不断) 时,证明:存在
时,证明:存在 ,使
,使 ;
; 的
的 ,且
,且 ,使
,使 ,证明:
,证明: .
.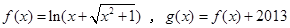 ,下列命题:
,下列命题: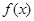 的定义域为
的定义域为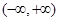 ;
; 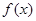 在
在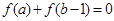 ,则
,则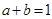 ;
;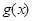 在
在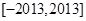 的最大值为M,最小值为m,则M+m=2013
的最大值为M,最小值为m,则M+m=2013 米.
米.
 是定义在
是定义在 上的偶函数,且对任意的
上的偶函数,且对任意的
 .当
.当 时,
时, .若直线
.若直线 与函数
与函数 的图象有两个不同的公共点,则实数
的图象有两个不同的公共点,则实数 的值为( )
的值为( )




