题目内容
15. 若一个空间几何体的三个视图都是直角边长为1的等腰直角三角形,则这个空间几何体的外接球的表面积和内切球的表面积之比是( )
若一个空间几何体的三个视图都是直角边长为1的等腰直角三角形,则这个空间几何体的外接球的表面积和内切球的表面积之比是( )| A. | $\frac{18+9\sqrt{3}}{2}$ | B. | 18+9$\sqrt{3}$ | C. | 3 | D. | 9 |
分析 根据题意,得出该几何体是一个三棱锥,把此三棱锥补成正方体,求出它的外接球半径R,
再利用等积法求出它的内切球半径r,即可计算该三棱锥外接球与内切球的表面积比.
解答 解:由几何体的三视图知:该几何体是一个三棱锥,如图所示,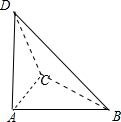 且AB=AC=AD=1,AB,AC,AD两两垂直;
且AB=AC=AD=1,AB,AC,AD两两垂直;
把此三棱锥补成正方体,则该三棱锥的外接球直径为正方体的对角线,
即l=2R,∴外接球半径为R=$\frac{l}{2}$=$\frac{\sqrt{3}}{2}$;
设三棱锥的内切球半径为r,
则三棱锥的体积为
$\frac{1}{3}$r(S△ABC+S△ABD+S△ADC+S△BCD)=V三棱锥D-ABC,
即$\frac{1}{3}$r($\frac{1}{2}$×1×1+$\frac{1}{2}$×1×1+$\frac{1}{2}$×1×1+$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$×$\sqrt{2}$×$\sqrt{2}$)=$\frac{1}{3}$×$\frac{1}{2}$×1×1×1,
解得r=$\frac{1}{3+\sqrt{3}}$;
∴该三棱锥的外接球与内切球的表面积之比为
$\frac{4{πR}^{2}}{4{πr}^{2}}$=$\frac{{R}^{2}}{{r}^{2}}$=$\frac{{(\frac{\sqrt{3}}{2})}^{2}}{{(\frac{1}{3+\sqrt{3}})}^{2}}$=$\frac{18+9\sqrt{3}}{2}$.
故选:A.
点评 本题考查了三棱锥的三视图、正方体外接球与内切球的表面积的计算问题,是基础题目.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
5.已知sin($\frac{π}{2}$+θ)=$\frac{1}{3}$,则2sin2$\frac{θ}{2}$-1等于( )
| A. | $\frac{\sqrt{2}}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | ±$\frac{2\sqrt{2}}{3}$ |
20.已知函数f(x)=x2+mx+m+1(m>5)的两个零点分别为tanα,tanβ,且α,β∈(-$\frac{π}{2}$,$\frac{π}{2}$),则α+β的值为( )
| A. | $\frac{π}{4}$ | B. | -$\frac{π}{4}$ | C. | $\frac{3}{4}π$ | D. | -$\frac{3}{4}π$ |
6.复数z满足$z=\frac{2+i}{i}+i$,则|z|=( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |