Question

已知⊙C：x²+(y-1)²=5，直线：mx-y+1-m=0

（1）求证：对m∈R，直线与圆C总有两个不同交点A、B；

（2）求弦AB中点M轨迹方程，并说明其轨迹是什么曲线？

（3）若定点P(1,1)分弦AB为，求方程。

Answer 1

解：（1）圆心C（0，1），半径r=，则圆心到直线L的距离d=，          

∴d＜r，∴对m直线L与圆C总头两个不同的交点；（或用直线恒过一个定点，且这个定点在圆内）

（2）设中点M（x，y），因为L：m（x-1）-（y-1）=0恒过定点P（1，1）

∴，又，k_ABK_NC=-1，

∴，整理得；x²+y²-x-2y+1=0，

即：=，表示圆心坐标是（），半径是的圆；

（3）设A（x₁，y₁），B（x₂，y₂）解方程组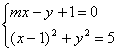

得（1+m²）x²-2m²x+m²-5=0，∴，①  又

∴（x₂-1，y₂-1）=2（1-x₁，1-y₁），即：2x₁+x₂=3   ②

联立①②解得，则，即A（）

将A点的坐标带入圆的方程得：m=±1，∴直线方程为x-y=0和x+y-2=0