题目内容
13.已知函数f(x)=x2-kx+1,若存在α∈(0,$\frac{π}{2}$),使f(sinα)=f(cosα)(1)当k=$\frac{1}{5}$时,求tanα的值
(2)在(1)的成立的基础上,求$\frac{{2{{sin}^2}α-2sinα•cosα}}{1+tanα}$的值.
分析 (1)当k=$\frac{1}{5}$时,求tanα的值
(2)根据条件分别求出sinα,cosα,tanα的值代入即可.
解答 解:(1)把k=$\frac{1}{5}$代入方程得:f(x)=x2-$\frac{1}{5}$x+1,
∵f(sinα)=f(cosα),
∴sin2α-$\frac{1}{5}$sinα+1=cos2α-$\frac{1}{5}$cosα+1,
整理得:sinα+cosα=$\frac{1}{5}$,
两边平方得:1+2sinαcosα=$\frac{1}{25}$,即2sinαcosα=-$\frac{24}{25}$<0,
∴sinα>0,cosα<0,
解得:sinα=$\frac{4}{5}$,cosα=-$\frac{3}{5}$,
则tanα=-$\frac{4}{3}$;
(2)原式=$\frac{2×\frac{16}{25}-2×\frac{4}{5}×(-\frac{3}{5})}{1-\frac{4}{3}}$=-$\frac{168}{25}$.
点评 此题考查了同角三角函数间的基本关系,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
2.若椭圆经过原点,且焦点为F1(-1,0)、F2(-3,0),则其离心率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
3.设a>0,b>0,若3是9a与27b的等比中项,则$\frac{3}{a}$+$\frac{2}{b}$的最小值为( )
| A. | 25 | B. | 24 | C. | 36 | D. | 12 |
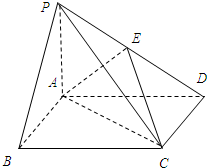 在如图所示四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是正方式,PA=AB=1,E是PD上的点,PB∥平面AEC,
在如图所示四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是正方式,PA=AB=1,E是PD上的点,PB∥平面AEC,