题目内容
设函数f(x)=x-xlnx,数列{an}满足0<a1<1,an+1=f(an)。
(1)证明:函数f(x)在区间(0,1)是增函数;
(2)证明:an<an+1<1;
(3)设b∈(a1,1),整数k≥ 。证明:ak+1>b。
。证明:ak+1>b。
(1)证明:函数f(x)在区间(0,1)是增函数;
(2)证明:an<an+1<1;
(3)设b∈(a1,1),整数k≥
 。证明:ak+1>b。
。证明:ak+1>b。解:(1)当0<x<1时,f'(x)=1-lnx-1=-ln-x>0
所以函数f(x)在区间(0,1)是增函数;
(2)当0<x<1时,f(x)=x-xlnx>x,
又由(1)及f(x)在x=1处连续知,
当0<x<1时,f(x)<f(1)=1,
因此,当0<x<1时,0<x<f(x)<1 ①
下面用数学归纳法证明: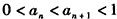 ②
②
(i)由0<a1<1,a2=f(a1),应用式①得0<a1<a2<1,即当n=1时,不等式②成立;
(ii)假设n=k时,不等式②成立,即
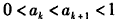
则由①可得
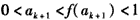
即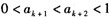
故当n=k+1时,不等式②也成立
综合(i)(ii)证得
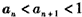 ;
;
(3)由(2)知,{an}逐项递增,故若存在正整数m≤k,使得
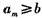 ,则
,则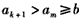
否则若am<b(m≤k),则由0<a1≤am<n<1(m≤k)知
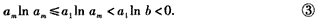
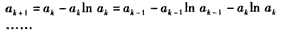
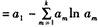
由③知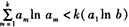
于是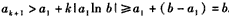 。
。
所以函数f(x)在区间(0,1)是增函数;
(2)当0<x<1时,f(x)=x-xlnx>x,
又由(1)及f(x)在x=1处连续知,
当0<x<1时,f(x)<f(1)=1,
因此,当0<x<1时,0<x<f(x)<1 ①
下面用数学归纳法证明:
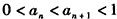 ②
②(i)由0<a1<1,a2=f(a1),应用式①得0<a1<a2<1,即当n=1时,不等式②成立;
(ii)假设n=k时,不等式②成立,即
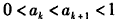
则由①可得
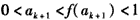
即
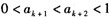
故当n=k+1时,不等式②也成立
综合(i)(ii)证得
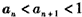 ;
;(3)由(2)知,{an}逐项递增,故若存在正整数m≤k,使得
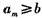 ,则
,则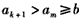
否则若am<b(m≤k),则由0<a1≤am<n<1(m≤k)知
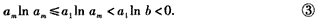
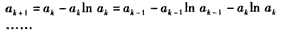
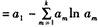
由③知
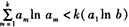
于是
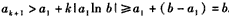 。
。
练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
设函数f(x)的定义域为A,若存在非零实数t,使得对于任意x∈C(C⊆A),有x+t∈A,且f(x+t)≤f(x),则称f(x)为C上的t低调函数.如果定义域为[0,+∞)的函数f(x)=-|x-m2|+m2,且 f(x)为[0,+∞)上的10低调函数,那么实数m的取值范围是( )
| A、[-5,5] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|