题目内容
设n阶方阵,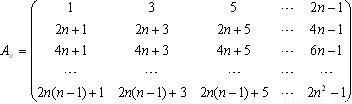 任取An中的一个元素,记为x1;划去x1所在的行和列,将剩下的元素按原来的位置关系组成n-1阶方阵An-1,任取An-1中的一个元素,记为x2;划去x2所在的行和列,…;将最后剩下的一个元素记为xn,记Sn=x1+x2+…+xn,则
任取An中的一个元素,记为x1;划去x1所在的行和列,将剩下的元素按原来的位置关系组成n-1阶方阵An-1,任取An-1中的一个元素,记为x2;划去x2所在的行和列,…;将最后剩下的一个元素记为xn,记Sn=x1+x2+…+xn,则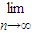
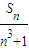 = .
= .
【答案】分析:取x1=1,x2=2n+3,x3=4n+5,由题设条件可知Sn=1+(2n+3)+(4n+5)+…+(2n2-1)=n3+n2,由此能够导出
 的值.
的值.
解答:解:不妨取x1=1,x2=2n+3,x3=4n+5,故
Sn=1+(2n+3)+(4n+5)+…+(2n2-1)
=[1+3+5+…+(2n-1)]+[2n+4n+…+(n-1)2n]
=n2+(n-1)×n2
=n3
故
 =
=
 =
=
 =1,
=1,
答案:1.
点评:本题考查高阶矩阵和数列的极限,解题时要认真审题,仔细解答,避免不必要的错误.

 的值.
的值.解答:解:不妨取x1=1,x2=2n+3,x3=4n+5,故
Sn=1+(2n+3)+(4n+5)+…+(2n2-1)
=[1+3+5+…+(2n-1)]+[2n+4n+…+(n-1)2n]
=n2+(n-1)×n2
=n3
故

 =
=
 =
=
 =1,
=1,答案:1.
点评:本题考查高阶矩阵和数列的极限,解题时要认真审题,仔细解答,避免不必要的错误.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
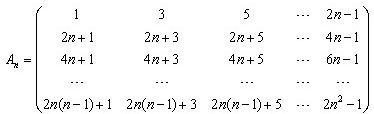
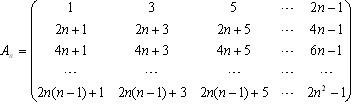 任取An中的一个元素,记为x1;划去x1所在的行和列,将剩下的元素按原来的位置关系组成n-1阶方阵An-1,任取An-1中的一个元素,记为x2;划去x2所在的行和列,…;将最后剩下的一个元素记为xn,记Sn=x1+x2+…+xn,则
任取An中的一个元素,记为x1;划去x1所在的行和列,将剩下的元素按原来的位置关系组成n-1阶方阵An-1,任取An-1中的一个元素,记为x2;划去x2所在的行和列,…;将最后剩下的一个元素记为xn,记Sn=x1+x2+…+xn,则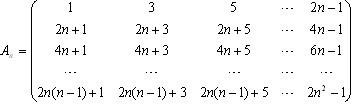 任取An中的一个元素,记为x1;划去x1所在的行和列,将剩下的元素按原来的位置关系组成n-1阶方阵An-1,任取An-1中的一个元素,记为x2;划去x2所在的行和列,…;将最后剩下的一个元素记为xn,记Sn=x1+x2+…+xn,则
任取An中的一个元素,记为x1;划去x1所在的行和列,将剩下的元素按原来的位置关系组成n-1阶方阵An-1,任取An-1中的一个元素,记为x2;划去x2所在的行和列,…;将最后剩下的一个元素记为xn,记Sn=x1+x2+…+xn,则
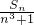 =________.
=________.