题目内容
已知f1(x)=
,对任意n∈N*,恒有fn+1(x)=f1[fn(x)],则f2014(2013)=( )
| x-1 |
| x+1 |
分析:由条件求得则f2(x)=
,f3(x)=
,f4(x)=x,f5=f1[f4(x)]=f1(x),故fn(x)是以4为周期的周期函数再根据f2014(2013)=f2(2013),运算求得结果.
| -1 |
| x |
| 1+x |
| 1-x |
解答:解:已知f1(x)=
,对任意n∈N*,恒有fn+1(x)=f1[fn(x)],则f2(x)=f1[f1(x)]=
=
=
,
f3(x)=f1[f2(x)]=
=
=
,f4(x)=f1[f3(x)]=
=
=x,
f5=f1[f4(x)]=
=
=f1(x),故fn(x)是以4为周期的周期函数,
故f2014(2013)=f2(2013)=
,
故选D.
| x-1 |
| x+1 |
| f1(x)-1 |
| f1(x)+1 |
| ||
|
| -1 |
| x |
f3(x)=f1[f2(x)]=
| f2(x)-1 |
| f2(x)+1 |
| ||
|
| 1+x |
| 1-x |
| f3(x)-1 |
| f3(x)+1 |
| ||
|
f5=f1[f4(x)]=
| f4(x)-1 |
| f4(x)+1 |
| x-1 |
| x+1 |
故f2014(2013)=f2(2013)=
| -1 |
| 2013 |
故选D.
点评:本题主要考查利用函数的周期性求函数的值,属于基础题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
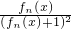 ,求证:F1(2)+F2(2)+…Fn(2)<1;
,求证:F1(2)+F2(2)+…Fn(2)<1; ,求证:F1(2)+F2(2)+…Fn(2)<1;
,求证:F1(2)+F2(2)+…Fn(2)<1;