题目内容
已知函数f(x)=xsinx+cosx,其导函数k=f'(x)的图象大致为
- A.
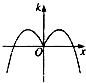
- B.
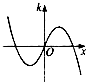
- C.
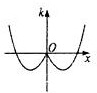
- D.
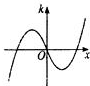
B
分析:由题可得f′(x)=sinx+xcosx-sinx=xcosx令g(x)=xcosx可观察出过(0,0)点下面只需利用导数判断其在各段的单调性即可得出结果.
解答:∵f(x)=xsinx+cosx
∴f′(x)=sinx+xcosx-sinx=xcosx
令g(x)=xcosx且g(0)=0
∴g(x)过(0,0)点
∵g′(x)=cosx-xsinx
∴g′′(x)=-2sinx-xcosx
∴当x∈(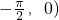 时g′′(x)>0故g′(x)单调递增
时g′′(x)>0故g′(x)单调递增
则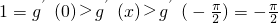
故存在a 使得g′(a)=0
使得g′(a)=0
所以当x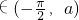 时g′(x)<0,g(x)单调递减
时g′(x)<0,g(x)单调递减
当x∈(a,0)时g′(x)>0,g(x)单调递增
当x∈(0, )时g′′(x)<0故g′(x)单调递减
)时g′′(x)<0故g′(x)单调递减
则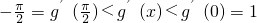
故存在b∈(0, )时使得g′(b)=0
)时使得g′(b)=0
所以当x∈(0,b)时g′(x)>0,g(x)单调递增
当x∈(b, )时g′(x)<0,g(x)单调递减
)时g′(x)<0,g(x)单调递减
综上:f′(x)在(- ,a)单调递减,在(a,b)单调递增,在(b,
,a)单调递减,在(a,b)单调递增,在(b, )单调递减.结合图象可知选B
)单调递减.结合图象可知选B
故答案选B
点评:本题主要考查了利用导数判断函数的单调性.此题关键是不易判断出g′(x)的正负因此采用再求导数即g′′(x)=-2sinx-xcosx可判断出x∈(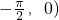 时g′′(x)>0故g′(x)单调递增进而可得出g′(x)的值有正有负再结合根的存在性定理可得出g′(x)>0的区间即g(x)的增区间和g′(x)<0的区间即减区间而x∈(0,
时g′′(x)>0故g′(x)单调递增进而可得出g′(x)的值有正有负再结合根的存在性定理可得出g′(x)>0的区间即g(x)的增区间和g′(x)<0的区间即减区间而x∈(0, )的单调性可同理讨论!
)的单调性可同理讨论!
分析:由题可得f′(x)=sinx+xcosx-sinx=xcosx令g(x)=xcosx可观察出过(0,0)点下面只需利用导数判断其在各段的单调性即可得出结果.
解答:∵f(x)=xsinx+cosx
∴f′(x)=sinx+xcosx-sinx=xcosx
令g(x)=xcosx且g(0)=0
∴g(x)过(0,0)点
∵g′(x)=cosx-xsinx
∴g′′(x)=-2sinx-xcosx
∴当x∈(
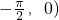 时g′′(x)>0故g′(x)单调递增
时g′′(x)>0故g′(x)单调递增则
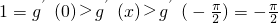
故存在a
 使得g′(a)=0
使得g′(a)=0所以当x
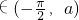 时g′(x)<0,g(x)单调递减
时g′(x)<0,g(x)单调递减当x∈(a,0)时g′(x)>0,g(x)单调递增
当x∈(0,
 )时g′′(x)<0故g′(x)单调递减
)时g′′(x)<0故g′(x)单调递减则
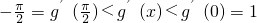
故存在b∈(0,
 )时使得g′(b)=0
)时使得g′(b)=0所以当x∈(0,b)时g′(x)>0,g(x)单调递增
当x∈(b,
 )时g′(x)<0,g(x)单调递减
)时g′(x)<0,g(x)单调递减综上:f′(x)在(-
 ,a)单调递减,在(a,b)单调递增,在(b,
,a)单调递减,在(a,b)单调递增,在(b, )单调递减.结合图象可知选B
)单调递减.结合图象可知选B故答案选B
点评:本题主要考查了利用导数判断函数的单调性.此题关键是不易判断出g′(x)的正负因此采用再求导数即g′′(x)=-2sinx-xcosx可判断出x∈(
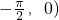 时g′′(x)>0故g′(x)单调递增进而可得出g′(x)的值有正有负再结合根的存在性定理可得出g′(x)>0的区间即g(x)的增区间和g′(x)<0的区间即减区间而x∈(0,
时g′′(x)>0故g′(x)单调递增进而可得出g′(x)的值有正有负再结合根的存在性定理可得出g′(x)>0的区间即g(x)的增区间和g′(x)<0的区间即减区间而x∈(0, )的单调性可同理讨论!
)的单调性可同理讨论! 
练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|