题目内容
函数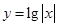 是( )
是( )
A.偶函数,在区间 上单调递增 上单调递增 | B.偶函数,在区间 上单调递减 上单调递减 |
C.奇函数,在区间 上单调递增 上单调递增 | D.奇函数,在区间 上单调递减 上单调递减 |
B
解析试题分析: 由于函数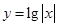 中,以-x代x解析式不变,那么可知函数是一个偶函数,同时在x>0时,原解析式为y=lgx,那么根据对数函数的性质可知,在定义域内递增函数,故可知对称区间上为减函数,因此偶函数,在区间
中,以-x代x解析式不变,那么可知函数是一个偶函数,同时在x>0时,原解析式为y=lgx,那么根据对数函数的性质可知,在定义域内递增函数,故可知对称区间上为减函数,因此偶函数,在区间 上单调递减,选B.
上单调递减,选B.
考点:本题主要考查了对数函数的图像和性质的运用,以及图像变换的问题。
点评:解决该试题的关键是对于已知函数的图像求解,和对于绝对值函数的性质的准确分析和 运用。

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
函数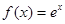 (
(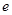 为自然对数的底数)对任意实数
为自然对数的底数)对任意实数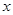 、
、 ,都有( )
,都有( )
A.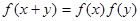 | B.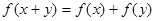 |
C.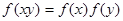 | D.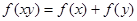 |
若 ,则
,则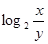 的值为( )
的值为( )
| A.0 | B.2 | C.-2 | D.0或2 |
若函数 的定义域为[0 , m],值域为
的定义域为[0 , m],值域为 ,则m的取值范围是( )
,则m的取值范围是( )
| A.(0 , 4] | B.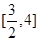 | C. | D. ) ) |
若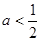 ,则化简
,则化简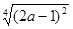 的结果是( )
的结果是( )
A.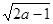 | B.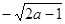 | C.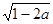 | D.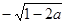 |
指数函数y=a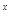 的图像经过点(2,16)则a的值是
的图像经过点(2,16)则a的值是
A.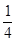 | B.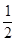 | C.2 | D.4 |
若方程 在(0,1)内恰有一解,则
在(0,1)内恰有一解,则 的取值范围是
的取值范围是
A. | B. | C. | D. |
设函数 ,则
,则 =( )
=( )
| A.2 | B.6 | C.8 | D.4 |
 的图象只可能是 ( )
的图象只可能是 ( )