题目内容
下列函数中，值域为（0，+∞）的是（ ）A．y=2x2-1
B．y=lg（x2+1）
C．
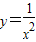
D．
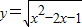
【答案】分析：利用基本函数的单调性即可得出．
解答：解：A．∵y=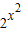
-1≥2-1=0，∴函数的值域为[0，+∞）；
B．∵x2+1≥1，∴y=ln（x2+1）≥0，∴函数的值域为[0，+∞）；
C．其定义域为{x|x≠0}，∴x2＞0，∴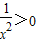
，因此函数的值域为（0，+∞）；
D.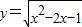
，∵x2-2x-1≥0，解得
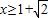，或
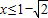，∴y≥0，因此函数的值域为[0，+∞）．
综上可知：只有C满足条件．
故选C．
点评：熟练掌握基本函数的单调性是解题的关键．
解答：解：A．∵y=
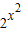-1≥2-1=0，∴函数的值域为[0，+∞）；B．∵x2+1≥1，∴y=ln（x2+1）≥0，∴函数的值域为[0，+∞）；
C．其定义域为{x|x≠0}，∴x2＞0，∴
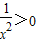，因此函数的值域为（0，+∞）；D.
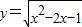，∵x2-2x-1≥0，解得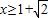，或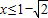，∴y≥0，因此函数的值域为[0，+∞）．综上可知：只有C满足条件．
故选C．
点评：熟练掌握基本函数的单调性是解题的关键．
练习册系列答案
相关题目
下列函数中，值域为（0，+∞）的是（ ）
A、y=(
| ||
B、y=
| ||
C、y=
| ||
D、y=2
|