Question

已知函数f（x）=mx²-2x+1，g（x）=mx，若对任意实数x，f（x）与g（x）的值至少有一个为正数，则实数m的取值范围是

{m|m＞0}

．

Answer 1

分析：当m＜0时，显然不满足条件．经过检验，当m=0时，也不满足条件．当m＞0时，数形结合可得故满足条件，从而求得实数m的取值范围．

解答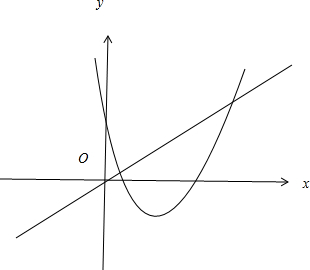：解：当m＜0时，显然不满足条件．
当m=0时，函数f（x）=mx²-2x+1=-2x+1，g（x）=mx=0，显然不满足条件．
当m＞0时，对于函数f（x）=mx²-2x+1，对称轴为x=

1

m

＞0，且f（0）=1，而g（x）=mx，故满足条件，如图所示：
综上可得，实数m的取值范围是{m|m＞0}，
故答案为 {m|m＞0}．

点评：本题主要考查对二次函数图象的理解，对于一元二次不等式，一定要注意其开口方向、对称轴和判别式，体现了数形结合的数学思想，属于中档题．