Question

如图,在△ABC中,已知b=20,A=45°,当a分别等于10、15、25时,求B和c.

Answer 1

解析:(1)当a=10时,根据正弦定理:=,即sinB==1,

∴B=90°,c=a=10.

(2)当a=15,

根据正弦定理:=,即sinB==,

∴B=arcsin或B=π-arcsin.

若B为锐角,则cosB=,

sinC=sin［π-(A+B)］=sin(A+B)

=sinAcosB+cosAsinB

=·+·=,

c==10+5.

若B为钝角,则cosB=-,

sinC=sin(A+B)=sinAcosB+cosAsinB

=·(-)+·=,

∴c==10-5.

(3)当a=25,由a＞b,

∴A＞B,即B为锐角.

根据正弦定理:=,

∴sinB==.

∴B=arcsin,cosB=.

∴sinC=sin［π-(A+B)］

=sin(A+B)=sinAcosB+cosAsinB

=×+×=.

∴c==

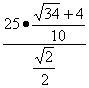
=5+10.

点评：根据正弦定理可已知两角一边解三角形;可已知两边和一边的对角解三角形,通过本题可看到已知两边和一边对角解三角形的情况和具体解法.