题目内容
若ξ～N（-1，σ2），且P（-3≤ξ≤-1）=0.4，则P（ξ≥1）等于（ ）
| A、0.1 | B、0.2 |
| C、0.3 | D、0.4 |
考点：正态分布曲线的特点及曲线所表示的意义
专题：计算题,概率与统计
分析：利用ξ～N（-1，σ2），可得图象关于x=-1对称，结合P（-3≤ξ≤-1）=0.4，即可求得结论．
解答：
解：∵ξ～N（-1，σ2），∴图象关于x=-1对称
∵P（-3≤ξ≤-1）=0.4，
∴P（-1≤ξ≤1）=0.4，
∴P（ξ≥1）=0.5-0.4=0.1
故选：A．
∵P（-3≤ξ≤-1）=0.4，
∴P（-1≤ξ≤1）=0.4，
∴P（ξ≥1）=0.5-0.4=0.1
故选：A．
点评：本题考查正态分布曲线的对称性，考查学生的计算能力，属于基础题．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
下列为某班级英语及数学成绩的统计，学生共有50人，成绩实行5分制，如表中英语成绩为4分，数学成绩为2分的人数为5人，将全班学生的姓名卡混在一起，任取一枚，则该卡片上的学生的数学、英语成绩和不低于8分的概率是（ ）
| 数学 人数 英语 | 5 | 4 | 3 | 2 | 1 |
| 5 | 1 | 3 | 1 | 0 | c |
| 4 | 1 | 0 | 7 | 5 | 1 |
| 3 | 2 | 1 | 0 | 9 | 1 |
| 2 | 1 | b | 6 | 0 | a |
| 1 | 0 | 0 | 1 | 1 | 3 |
| A、0.16 | B、0.20 |
| C、0.25 | D、0.28 |
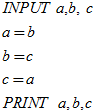以下程序输入2，3，4运行后，输出的结果是