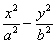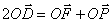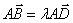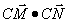题目内容
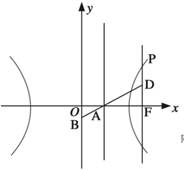
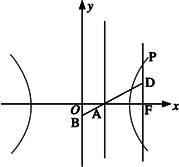
如图,已知双曲线![]() (a>0,b>0)其右准线交x轴于点A,双曲线虚轴的下端点为B,过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于点P,若点D满足:
(a>0,b>0)其右准线交x轴于点A,双曲线虚轴的下端点为B,过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于点P,若点D满足:![]() (O为原点)且
(O为原点)且![]() (λ≠0)
(λ≠0)
(Ⅰ)求双曲线的离心率;
(Ⅱ)若a=2,过点B的直线l交双曲线于M、N两点,问在y轴上是否存在定点C,使![]() 为常数,若存在,求出C点的坐标,若不存在,请说明理由.
为常数,若存在,求出C点的坐标,若不存在,请说明理由.
答案:
解析:
解析:
|
(Ⅰ)∵B(0,-b),A( ∵2 ∴(c, ∴而 得a=2b∴e= (Ⅱ)∵a=2而e= ∴B(0,-1) 假设存在定点C(0,n)使 设MN的方程为y=kx-1 ② 6分 由②代入①得 由题意得 设M( 而 = 整理得:[4 对满足 ∴ 故存在y轴上的定点C(0,4),使 |

练习册系列答案
相关题目
 如图,已知双曲线以长方形ABCD的顶点A,B为左、右焦点,且过C,D两顶点.若AB=4,BC=3,则此双曲线的标准方程为
如图,已知双曲线以长方形ABCD的顶点A,B为左、右焦点,且过C,D两顶点.若AB=4,BC=3,则此双曲线的标准方程为 (2008•湖北模拟)如图,已知双曲线
(2008•湖北模拟)如图,已知双曲线