题目内容
若在锐角△ABC中(a,b,c分别为内角A,B,C的对边),满足a2+b2=6abcosC,且sin2C=2sinAsinB,则角C的值为________.

分析:利用正弦定理与余弦定理可求得cosC=
 ,从而可求得角C的值.
,从而可求得角C的值.解答:由正弦定理有:sin2C=2sinAsinB?c2=2ab,
由余弦定理有:a2+b2=c2+2abcosC=c2(1+cosC)①
又a2+b2=6abcosC=3c2cosC②
由①②得1+cosC=3cosC
?cosC=
 ,
,又0<C<π,
∴C=
 .
.故答案为

点评:本题考查正弦定理与余弦定理,考查代换与解方程的能力,属于中档题.

练习册系列答案
相关题目
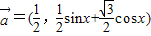 ,
,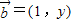 ,且
,且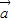 ∥
∥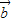 .设函数y=f(x).
.设函数y=f(x).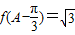 ,边
,边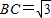 ,求△ABC周长的最大值.
,求△ABC周长的最大值.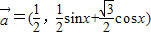 ,
,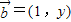 ,且
,且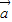 ∥
∥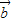 .设函数y=f(x).
.设函数y=f(x).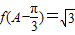 ,边
,边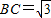 ,求△ABC周长的最大值.
,求△ABC周长的最大值. ,
, ,且
,且 ∥
∥ .设函数y=f(x).
.设函数y=f(x). ,边
,边 ,求△ABC周长的最大值.
,求△ABC周长的最大值.