题目内容
平面直角坐标系xOy中,曲线y=ax(a>0且a≠1)在第二象限的部分都在不等式(x+y-1)(x-y+1)>0表示的平面区域内,则a的取值范围是
- A.0<a≤

- B.
 ≤a<1
≤a<1 - C.1<a≤e
- D.a≥e
C
分析:先画出不等式(x+y-1)(x-y+1)>0表示的平面区域,然后根据曲线y=ax(a>0且a≠1)在第二象限的部分都在不等式(x+y-1)(x-y+1)>0表示的平面区域内,则考虑零界位置,直线x-y+1=0与曲线y=ax相切与点(0,1)是零界位置,求出此时a的值,从而得到结论.
解答:画出不等式(x+y-1)(x-y+1)>0表示的平面区域

曲线y=ax(a>0且a≠1)在第二象限的部分都在不等式(x+y-1)(x-y+1)>0表示的平面区域内
∴a>1,直线x-y+1=0与曲线y=ax相切与点(0,1)是零界位置
而(ax)′=axlna,则lna=1即a=e
∴1<a≤e
故选C.
点评:本题主要考查了二元一次不等式(组)与平面区域,以及利用导数研究曲线上某点切线方程,属于中档题.
分析:先画出不等式(x+y-1)(x-y+1)>0表示的平面区域,然后根据曲线y=ax(a>0且a≠1)在第二象限的部分都在不等式(x+y-1)(x-y+1)>0表示的平面区域内,则考虑零界位置,直线x-y+1=0与曲线y=ax相切与点(0,1)是零界位置,求出此时a的值,从而得到结论.
解答:画出不等式(x+y-1)(x-y+1)>0表示的平面区域

曲线y=ax(a>0且a≠1)在第二象限的部分都在不等式(x+y-1)(x-y+1)>0表示的平面区域内
∴a>1,直线x-y+1=0与曲线y=ax相切与点(0,1)是零界位置
而(ax)′=axlna,则lna=1即a=e
∴1<a≤e
故选C.
点评:本题主要考查了二元一次不等式(组)与平面区域,以及利用导数研究曲线上某点切线方程,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
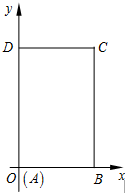 如图,在平面直角坐标系xOy中,已知矩形ABCD的两边AB,CD分别落在x轴、y轴的正半轴上,且AB=2,AD=4,点A与坐标原点重合.现将矩形折叠,使点A落在线段DC上,若折痕所在的直线的斜率为k,试写出折痕所在直线的方程及k的范围.
如图,在平面直角坐标系xOy中,已知矩形ABCD的两边AB,CD分别落在x轴、y轴的正半轴上,且AB=2,AD=4,点A与坐标原点重合.现将矩形折叠,使点A落在线段DC上,若折痕所在的直线的斜率为k,试写出折痕所在直线的方程及k的范围.