题目内容
若函数f（x）=x2-2|x|-2a-1（x∈R）有四个不同的零点，则实数a的取值范围是________．
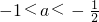
分析：将方程的零点问题转化成函数的交点问题，作出函数的图象得到a的范围．
解答：
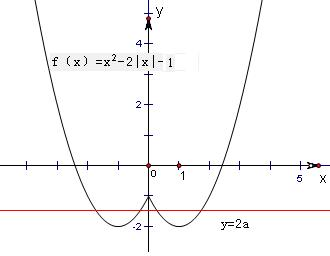解：令f（x）=x2-2|x|-2a-1=0，得2a=x2-2|x|-1．
作出y=x2-2|x|-1与y=2a的图象，如图．
要使函数f（x）=x2-2|x|-2a-1有四个零点，
则y=x2-2|x|-1与y=2a的图象有四个不同的交点，有-2＜2a＜-1，
所以
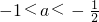．故答案为：
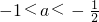
点评：本题考查等价转化的能力、利用数学结合解题的数学思想方法是重点，属中档题．
练习册系列答案
相关题目