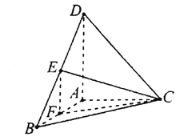
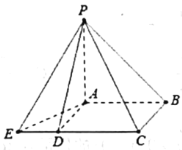
题目内容
【题目】在平面直角坐标系xOy中,点![]() 满足方程
满足方程![]() .
.
(1)求点M的轨迹C的方程;
(2)作曲线C关于![]() 轴对称的曲线,记为
轴对称的曲线,记为![]() ,在曲线C上任取一点
,在曲线C上任取一点![]() ,过点P作曲线C的切线l,若切线l与曲线
,过点P作曲线C的切线l,若切线l与曲线![]() 交于A,B两点,过点A,B分别作曲线
交于A,B两点,过点A,B分别作曲线![]() 的切线
的切线![]() ,
,![]() ,且
,且![]() ,
,![]() 的交点为Q,试问以Q为直角的
的交点为Q,试问以Q为直角的![]() 是否存在,若存在,求出点P的坐标;若不存在,请说明理由.
是否存在,若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ,(2)存在,
,(2)存在,![]() 或
或![]()
【解析】
(1)平方化简![]() ,即可求解;
,即可求解;
(2)根据导数的几何意义求出切线l的方程,与曲线![]() 方程联立,由韦达定理,确定两交点A,B坐标关系,再利用导数的几何意义,求出切线
方程联立,由韦达定理,确定两交点A,B坐标关系,再利用导数的几何意义,求出切线![]() ,
,![]() 的方程,并联立求出Q点坐标,
的方程,并联立求出Q点坐标,
利用![]() ,结合A,B坐标关系,即可求解.
,结合A,B坐标关系,即可求解.
(1)由![]() ,
,
两边平方并化简,得![]() ,即
,即![]() ,
,
所以点M的轨迹C的方程为![]() .
.
(2)依题可设点![]() ,
,![]() ,
,
曲线C切于点P的切线l的斜率为![]() ,
,
切线l的方程为![]() ,
,
整理得![]()
依题可知曲线![]() ,
,
联立方程组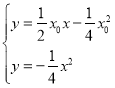
![]() ,
,![]() ,
,
设![]() ,
,![]() ,所以
,所以![]() ,
,![]() .(*)
.(*)
设曲线![]() 上点
上点![]() 处的切线斜率为
处的切线斜率为![]() ,
,
切线方程为![]() ,整理得
,整理得![]() ,
,
同理可得曲线![]() 上点
上点![]() 处的切线方程为
处的切线方程为![]() ,
,
联立方程组 ,
,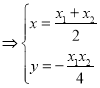 ,
,
又由(*)式得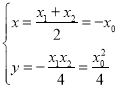 ,
,
所以![]() ,
,![]() 的交点Q的坐标为
的交点Q的坐标为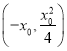 ,
,
假设以Q为直角的![]() 存在,则有
存在,则有![]() ,
,
而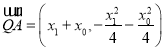 ,
,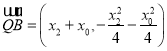 ,
,
所以由![]() ,得
,得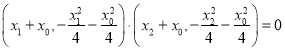 ,
,
即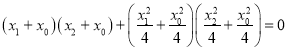 ,
,
即![]() ,
,
化简得![]() ,
,
因为由题得![]() ,所以
,所以![]() 或
或![]() ,
,
所以点P的坐标为![]() 或
或![]() .
.

【题目】黄冈“一票通”景区旅游年卡,是由黄冈市旅游局策划,黄冈市大别山旅游公司推出的一项惠民工程,持有旅游年卡一年内可不限次畅游全市19家签约景区.为了解市民每年旅游消费支出情况![]() 单位:百元
单位:百元![]() ,相关部门对已游览某签约景区的游客进行随机问卷调查,并把得到的数据列成如表所示的频数分布表:
,相关部门对已游览某签约景区的游客进行随机问卷调查,并把得到的数据列成如表所示的频数分布表:
组别 |
|
|
|
|
|
频数 | 10 | 390 | 400 | 188 | 12 |
![]() 求所得样本的中位数
求所得样本的中位数![]() 精确到百元
精确到百元![]() ;
;
![]() 根据样本数据,可近似地认为市民的旅游费用支出服从正态分布
根据样本数据,可近似地认为市民的旅游费用支出服从正态分布![]() ,若该市总人口为750万人,试估计有多少市民每年旅游费用支出在7500元以上;
,若该市总人口为750万人,试估计有多少市民每年旅游费用支出在7500元以上;
![]() 若年旅游消费支出在
若年旅游消费支出在![]() 百元
百元![]() 以上的游客一年内会继续来该景点游玩现从游客中随机抽取3人,一年内继续来该景点游玩记2分,不来该景点游玩记1分,将上述调查所得的频率视为概率,且游客之间的选择意愿相互独立,记总得分为随机变量X,求X的分布列与数学期望.
以上的游客一年内会继续来该景点游玩现从游客中随机抽取3人,一年内继续来该景点游玩记2分,不来该景点游玩记1分,将上述调查所得的频率视为概率,且游客之间的选择意愿相互独立,记总得分为随机变量X,求X的分布列与数学期望.
![]() 参考数据:
参考数据:,
![]() ;
;![]()