题目内容
某湖滨住宅小区为了营造一个优雅、舒适的生活环境,计划建造一个八边形的休闲花园,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的面积为200 m2的十字形地域,且计划在正方形MNPK上建一座花坛,造价为4 200元/m2,在四个相同的矩形上(右图阴影部分)铺花岗岩路面,造价为210元/m2,再在四个三角形空地上铺草坪,造价为80元/m2.
(1)设AD长为x m,试写出总造价Q关于x的函数关系式;
(2)问当x取何值时,总造价最小,并求出这个最小值.
解：(1)设AM=y,AD=x,则x2+4xy=200,
所以y=
.
所以Q=4 200x2+210·4xy+80·2y2=38 000+4 000x2+
(0＜x＜10
).
(2)因为x＞0,所以Q≥38 000+2·
=118 000,
当且仅当4 000x2=
,即x=
时,等号成立.
故当x=
m时,可使总造价Q最小,最小值为118 000元.
练习册系列答案
世纪百通期末金卷系列答案
相关题目
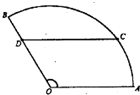如图，某住宅小区的平面图呈圆心角为120°的扇形AOB，C是该小区的一个出入口，且小区里有一条平行于AO的小路CD．已知某人从O沿OD走到D用了2分钟，从D沿着DC走到C用了3分钟．若此人步行的速度为每分钟50米，则该扇形的半径为
