题目内容

集合A₁，A₂，…，A_n的元素个数分别为1、2、…、n，它们的真子集个数分别为f（1），f（2），…，f（n），则f（1）+f（2）+…+f（n）=

A.
2ⁿ-2
B.
$数学公式$
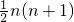
C.
2ⁿ⁺¹-2
D.
2ⁿ⁺¹-n-2

D
分析：根据题意，由集合的元素数目与其真子集数目的关系，可得f（n）=2ⁿ-1，可得f（1）+f（2）+…+f（n）=（2¹-1）+（2²-1）+…+（2ⁿ-1），由分组求和法计算可得答案．
解答：根据题意，若集合A_n的元素个数为n，则其真子集个数为2ⁿ-1，即有f（n）=2ⁿ-1，
则f（1）+f（2）+…+f（n）=（2¹-1）+（2²-1）+…+（2ⁿ-1）
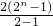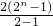=2¹+2²+2³+…2ⁿ-n= $\text{[math]}$ -n=2ⁿ⁺¹-n-2，
故选D．
点评：本题考查数列的求和与集合的元素数目与其真子集数目的关系，关键是分析得到f（n）=2n-1，再结合等比数列的求和公式，用分组求和法求解．

练习册系列答案

小学生寒假生活系列答案

小学生聪明屋寒暑假作业系列答案

寒假作业二十一世纪出版社系列答案

寒假作业上海科学技术出版社系列答案

全优寒假作业系列答案

轻松寒假复习加预习系列答案

成长记初中假期作业寒假云南教育出版社系列答案

强力推荐精品教辅高中新课标快乐假期寒系列答案

起跑线系列丛书新课标寒假作业系列答案

期末寒假一本通系列答案

相关题目

若集合A₁、A₂满足A₁∪A₂=A，则称（A₁，A₂）为集合的一种分拆，并规定：当且仅当A₁=A₂时，（A₁，A₂）与（A₂，A₁）为集合A的同一种分拆．请回答集合A={1，2，3，}的不同分拆有

集合A₁，A₂满足A₁∪A₂=A，则称（A₁，A₂）为集合A的一种分拆，并规定：当且仅当A₁=A₂时，（A₁，A₂）与（A₂，A₁）为集合A的同一种分拆，则集合A={a，b，c}的不同分拆种数为多少？

（2012•威海二模）若集合A₁，A₂…A_n满足A₁∪A₂∪…∪A_n=A，则称A₁，A₂…A_n为集合A的一种拆分．已知：
①当A₁∪A₂={a₁，a₂，a₃}时，有3³种拆分；
②当A₁∪A₂∪A₃={a₁，a₂，a₃，a₄}时，有7⁴种拆分；
③当A₁∪A₂∪A₃∪A₄={a₁，a₂，a₃，a₄，a₅}时，有15⁵种拆分；
…
由以上结论，推测出一般结论：
当A₁∪A₂∪…A_n={a₁，a₂，a₃，…a_n+1}有

（2ⁿ-1）ⁿ⁺¹

（2ⁿ-1）ⁿ⁺¹

对于集合{a₁，a₂，…，a_n}和常数a₀，定义：W=

sin2(a1-a0)+sin2(a2-a0)+…+sin2(an-a0)

为集合{a₁，a₂，…，a_n}相对a₀的“正弦方差”，则集合{

}相对a₀的“正弦方差”为

设项数均为k（k≥2，k∈N^*）的数列{a_n}、{b_n}、{c_n}前n项的和分别为S_n、T_n、U_n．已知集合{a₁，a₂，…，a_k，b₁，b₂，…，b_k}={2，4，6，…，4k-2，4k}．
（1）已知Un=2n+2n，求数列{c_n}的通项公式；
（2）若Sn-Tn=2n+2n（1≤n≤k，n∈N^*），试研究k=4和k≥6时是否存在符合条件的数列对（{a_n}，{b_n}），并说明理由；
（3）若an-bn=2n (1≤n≤k， n∈N*)，对于固定的k，求证：符合条件的数列对（{a_n}，{b_n}）有偶数对．