题目内容
△ABC的面积为1,| AB |
| a |
| AC |
| b |
| BP |
| 1 |
| 3 |
| b |
| 5 |
| 6 |
| a |
分析:在△ABC中,作出向量
=
-
,由向量的几何意义,三角形的面积公式,且△ABC的面积为1,可以求出△BCP的面积.
| BP |
| 1 |
| 3 |
| b |
| 5 |
| 6 |
| a |
解答: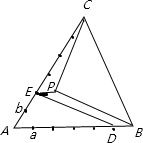 解:如图,在△ABC中,作出
解:如图,在△ABC中,作出
=
-
,
平移
=
,其中
=
,
△ABC的面积为:S=
|
|•
|sinA=
|
|•|
|sinA=1,
而△ADE,△CEP,平行四边形BDEP的面积和为:
|
•|
|sinA+
|
|•|
| sinCEP+|
|•|
|sinA=
|
|•|
|sinA+
|
|• |
|sinA+|
|• |
|sinA=
|
|• |
|sinA=
,
所以△BCP的面积为:1-
=
.
本题也可以通过左移点P:
+
个单位,下移
sinA个单位,到点A.知△BCP边BC上的高h2是△ABC边BC上的高h1的
,即△BCP的面积是△ABC的
.
故答案为:
.
 解:如图,在△ABC中,作出
解:如图,在△ABC中,作出| DE |
| 1 |
| 3 |
| b |
| 5 |
| 6 |
| a |
平移
| DE |
| BP |
| DB |
| 1 |
| 6 |
| a |
△ABC的面积为:S=
| 1 |
| 2 |
| AB |
| |AC |
| 1 |
| 2 |
| a |
| b |
而△ADE,△CEP,平行四边形BDEP的面积和为:
| 1 |
| 2 |
| AD| |
| AE |
| 1 |
| 2 |
| EP |
| EC |
| DB |
| AE |
| 1 |
| 2 |
| 5 |
| 6 |
| a |
| 1 |
| 3 |
| b |
| 1 |
| 2 |
| 1 |
| 6 |
| a |
| 2 |
| 3 |
| b |
| 1 |
| 6 |
| a |
| 1 |
| 3 |
| b |
| 1 |
| 4 |
| a |
| b |
| 1 |
| 2 |
所以△BCP的面积为:1-
| 1 |
| 2 |
| 1 |
| 2 |
本题也可以通过左移点P:
| 1 |
| 6 |
| a |
| 1 |
| 3 |
| a |
| 1 |
| 3 |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题通过作图得出向量的关系,从而求出三角形的面积.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
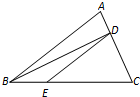 已知△ABC的面积为1,点D在AC上,DE∥AB,连接BD,设△DCE、△ABD、△BDE中面积最大者的值为y,则y的最小值为
已知△ABC的面积为1,点D在AC上,DE∥AB,连接BD,设△DCE、△ABD、△BDE中面积最大者的值为y,则y的最小值为