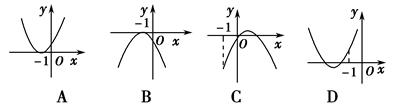
题目内容
函数f(x)=e2x+1的大致图象为 
C
解析试题分析:根据已知解析式可知,函数底数为e>1,那么是单调递增的函数,同时过定点x=0,Y=0,渐近线为y=1,可知答案为C.
考点:指数函数的图像
点评:根据解析式得到底数大于1,说明是增函数,同时过定点(0,2)得到,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设函数 ,则在下列区间中函数
,则在下列区间中函数 不存在零点的是
不存在零点的是
A.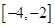 | B.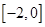 | C.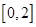 | D.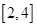 |
已知函数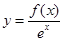 ,满足
,满足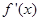 >
> ,则
,则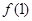 与
与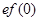 的大小关系是( )
的大小关系是( )
A.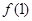 < <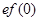 | B.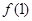 > >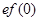 |
C.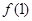 = = 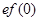 | D.不能确定 |
下列函数中,在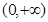 上为增函数的是 ( )
上为增函数的是 ( )
A.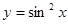 | B. |
C.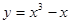 | D.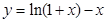 |
函数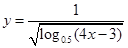 的定义域为( )
的定义域为( )
A.(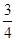 ,1) ,1) | B.(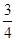 ,+∞) ,+∞) | C.(1,+∞) | D.(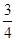 ,1)∪(1,+∞) ,1)∪(1,+∞) |
下列函数中是偶函数的是( )
A.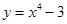 | B.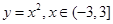 |
C.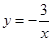 | D.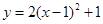 |
若函数 的零点与函数
的零点与函数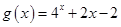 的零点之差的 绝对值不超过
的零点之差的 绝对值不超过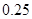 ,则
,则 可以是( )
可以是( )
A.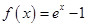 | B.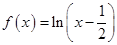 |
C.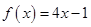 | D.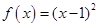 |
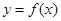 在区间
在区间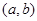 上的导函数为
上的导函数为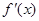 ,
,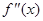 ,若在区间
,若在区间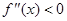 恒成立,则称函数
恒成立,则称函数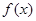 在区间
在区间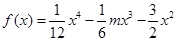 ,若对任意的实数
,若对任意的实数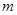 满足
满足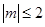 时,函数
时,函数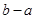 的最大值为
的最大值为