Question

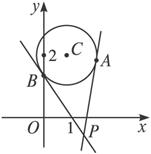
已知圆C:(x-1)²+(y-2)²=2,过点P(2,-1)作圆C的切线PA、PB,A、B为切点.

(1)求切线PA、PB所在直线的方程;

(2)求切线长|PA|;

(3)求∠APB的正弦值;

(4)求AB的方程.

Answer 1

解:(1)如下图,设过P点的切线方程为l:y+1=k(x-2),即kx-y-2k-1=0.

∵l与圆C相切,

∴d=r,

即.

∴k²-6k-7=0.

∴k=7或k=-1.

∴所求切线方程为y+1=7(x-2)或y+1=-(x-2),即7x-y-15=0或x+y-1=0.

(2)连结CA、PC,

在Rt△PAC中,|PC|=,|AC|=r=,

∴|PA|=2.

(3)在Rt△PCA中,设∠APC=θ,

∴sinθ=,cosθ=,sin2θ=2sinθ·cosθ=2×,即sin∠APB=.

(4)易得以PC为直径的圆的方程为(x-)²+(y-)²=.

将其与已知圆(x-1)²+(y-2)²=2联立,相减可得出公共弦AB所在直线的方程:4x-12y+27=0.