题目内容
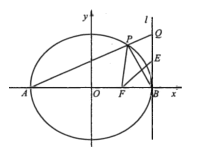
【题目】在平面直角坐标系xOy中,己知椭圆C:![]() 的左、右顶点为A,B,右焦点为F.过点A且斜率为k(
的左、右顶点为A,B,右焦点为F.过点A且斜率为k(![]() )的直线交椭圆C于另一点P.
)的直线交椭圆C于另一点P.
(1)求椭圆C的离心率;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)设直线l:![]() ,延长AP交直线l于点Q,线段BO的中点为E,求证:点B关于直线EF的对称点在直线PF上。
,延长AP交直线l于点Q,线段BO的中点为E,求证:点B关于直线EF的对称点在直线PF上。
【答案】(1)![]() (2)
(2)![]() (3)详见解析
(3)详见解析
【解析】
(1)根据椭圆的方程,结合椭圆离心率的求法,即可求出结果;
(2)先由题意,得到直线AP的方程为![]() 代入椭圆方程,求出点P的坐标,表示出
代入椭圆方程,求出点P的坐标,表示出![]() 与
与![]() ,进而可得出结果;
,进而可得出结果;
(3)由直线AP的方程与直线l的方程联立,求出![]() ,表示出直线EF的斜率,再由
,表示出直线EF的斜率,再由![]() 结合韦达定理,以及题中条件,表示出直线PF的斜率,再由题意,即可证明结论成立.
结合韦达定理,以及题中条件,表示出直线PF的斜率,再由题意,即可证明结论成立.
(1)因为椭圆C:![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
又![]() ,所以
,所以![]() ,
,![]() ,
,
所以椭圆C的离心率![]() .
.
(2)因为直线AP的斜率为![]() ,且过椭圆C的左顶点
,且过椭圆C的左顶点![]() ,
,
所以直线AP的方程为![]() .
.
代入椭圆C的方程![]() ,
,
得![]() ,即
,即![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
将![]() 代入
代入![]() ,得
,得![]() ,
,
所以点P的坐标为![]() .
.
又椭圆C的右顶点B(2t,0),
所以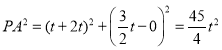 ,
,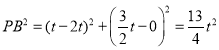 ,
,
所以![]() .
.
(3)直线AP的方程为![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,所以
,所以![]() .
.
因为E为线段BQ的中点,所以![]() ,
,
因为焦点F的坐标为(t,0),
所以直线EF的斜率![]() .
.
联立![]() 消y得,
消y得,![]() .
.
由于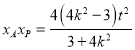 ,
,![]() ,
,
所以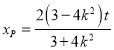 ,
,
所以点P的坐标为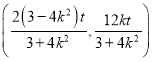 ,
,
所以直线PF的斜率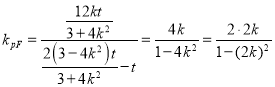 .
.
而直线EF的斜率为2k,
若设![]() ,则有
,则有![]() ,即
,即![]() ,
,
所以点B关于直线EF的对称点在直线PF上.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目