题目内容
【题目】已知立方和公式：
求函数
的值域；
求函数
，
的值域；
若任意实数x，不等式
恒成立，求实数a的取值范围．
【答案】（1）
；（2）
；（3）
【解析】
（1）先化简f（x）
sin（x
），再根据三角函数的性质即可求出，
（2）化简g（x）
，再设sinx+cosx＝t
sin（x），可得t∈[1，
]，可得g（x）＝h（t）
（
t），根据函数的单调性即可求出，
（3）化简sin6x+cos6x＝1﹣3sin2xcos2x，设sinxcosx＝t，即tsin2x，则
t
，则原不等式转化为3t2﹣at﹣1≤0在t∈[
，
]恒成立，即可求出a的范围
解：
，
，
，
，
故函数
的值域为，
，
设
，
，
，
，
，
，
，
，
易知函数
在
上为减函数，
，
，
函数
的值域为．
，
，
设
，即
，则
，
不等式
恒成立，
，在
恒成立，
即
在恒成立，
，
解得
，
故a的取值范围为
练习册系列答案
相关题目
【题目】关于函数
,有下列结论:
①
的定义域为(-1, 1); ②的值域为(
, 
);
③的图象关于原点成中心对称; ④在其定义域上是减函数;
⑤对的定义城中任意
都有
.
其中正确的结论序号为__________.
【题目】某种新产品投放市场一段时间后，经过调研获得了时间
（天数）与销售单价
（元）的一组数据，且做了一定的数据处理（如表），并作出了散点图（如图）
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中
，
.
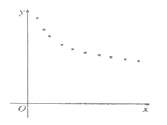
（1）根据散点图判断，
与
哪一个更适宜作价格关于时间的回归方程类型？（不必说明理由）
（2）根据判断结果和表中数据，建立关于的回归方程；
（3）若该产品的日销售量
（件）与时间的函数关系为
（
），求该产品投放市场第几天的销售额最高？最高为多少元？（结果保留整数）
附：对于一组数据
，
，
，
，
，其回归直线
的斜率和截距的最小二乘估计分别为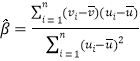
，
.
