题目内容
正方体ABCD-A′B′C′D′的棱长为2,则三棱锥A′-BC′D的体积 .
分析:根据要求几何体是由正方体削去4个相同的三棱锥而得,计算V正方体-4VC′-BCD可得答案.
解答:解:∵正方体ABCD-A′B′C′D′的棱长为2,
∴VA′-BC′D=V正方体-4VC′-BCD=23-4×
×
×2×2×2=
,
故答案是
.
∴VA′-BC′D=V正方体-4VC′-BCD=23-4×
| 1 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |
故答案是
| 8 |
| 3 |
点评:本题考查了用间接法求棱锥的体积,解答的关键是根据正方体的几何特征看出要求几何体是由正方体削去4个相同的三棱锥而得.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
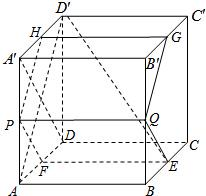 如图,在棱长为1的正方体ABCD-A′B′C′D′中,AP=BQ=b(0<b<1),截面PQEF∥A′D,截面PQGH∥AD′.
如图,在棱长为1的正方体ABCD-A′B′C′D′中,AP=BQ=b(0<b<1),截面PQEF∥A′D,截面PQGH∥AD′.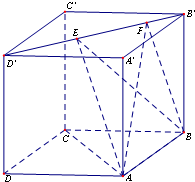 如图,正方体ABCD-A′B′C′D′的棱长为1,线段B′D′上有两个动点E,F且
如图,正方体ABCD-A′B′C′D′的棱长为1,线段B′D′上有两个动点E,F且 (2011•蓝山县模拟)如图,在正方体ABCD-A′B′C′D′中,异面直线BD与B′C所成角为
(2011•蓝山县模拟)如图,在正方体ABCD-A′B′C′D′中,异面直线BD与B′C所成角为