题目内容
已知圆x2+y2+mx- =0与抛物线y=
=0与抛物线y=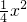 的准线相切,则m的值等于
的准线相切,则m的值等于
- A.±

- B.

- C.

- D.±

D
分析:由抛物线的方程找出P,写出抛物线的准线方程,因为准线方程与圆相切,所以圆心到直线的距离等于圆的半径,利用点到直线的距离公式列出关于m的方程,求出方程的解即可得到m的值.
解答:由抛物线的方程得到p=2,所以抛物线的准线为y=- =-1,
=-1,
将圆化为标准方程得: +y2=
+y2= ,圆心坐标为(-
,圆心坐标为(- ,0),圆的半径r=
,0),圆的半径r= ,
,
圆心到直线的距离d= =1=r=
=1=r= ,
,
化简得:m2=3,解得m=± .
.
故选D
点评:此题考查学生会求抛物线的准线方程,掌握直线与圆相切时所满足的条件,灵活运用点到直线的距离公式化简求值,是一道综合题.
分析:由抛物线的方程找出P,写出抛物线的准线方程,因为准线方程与圆相切,所以圆心到直线的距离等于圆的半径,利用点到直线的距离公式列出关于m的方程,求出方程的解即可得到m的值.
解答:由抛物线的方程得到p=2,所以抛物线的准线为y=-
 =-1,
=-1,将圆化为标准方程得:
 +y2=
+y2= ,圆心坐标为(-
,圆心坐标为(- ,0),圆的半径r=
,0),圆的半径r= ,
,圆心到直线的距离d=
 =1=r=
=1=r= ,
,化简得:m2=3,解得m=±
 .
.故选D
点评:此题考查学生会求抛物线的准线方程,掌握直线与圆相切时所满足的条件,灵活运用点到直线的距离公式化简求值,是一道综合题.

练习册系列答案
相关题目