题目内容
12. 如图,矩形ABCD的四个顶点的坐标分别为A(0,-1),B(π,-1),C(π,1),D(0,1),正弦曲线f(x)=sinx和余弦曲线g(x)=cosx在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是$\frac{1+\sqrt{2}}{2π}$.
如图,矩形ABCD的四个顶点的坐标分别为A(0,-1),B(π,-1),C(π,1),D(0,1),正弦曲线f(x)=sinx和余弦曲线g(x)=cosx在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是$\frac{1+\sqrt{2}}{2π}$.
分析 利用定积分计算公式,算出曲线y=sinx与y=cosx围成的区域包含在区域D内的图形面积为S=2π,再由定积分求出阴影部分的面积,利用几何概型公式加以计算即可得到所求概率
解答 解:根据题意,可得曲线y=sinx与y=cosx围成的区域,
其面积为${∫}_{\frac{π}{4}}^{π}(sinx-cosx)dx$=(-cosx-sinx)|${\;}_{\frac{π}{4}}^{π}$=1-(-$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{2}$)=1+$\sqrt{2}$;
又矩形ABCD的面积为2π,
由几何概型概率公式得该点落在阴影区域内的概率是$\frac{1+\sqrt{2}}{2π}$;
故答案为:$\frac{1+\sqrt{2}}{2π}$.
点评 本题给出区域和正余弦曲线围成的区域,求点落入指定区域的概率.着重考查了定积分计算公式、定积分的几何意义和几何概型计算公式等知识.

练习册系列答案
相关题目
4.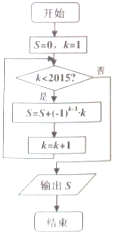 阅读如图所示的框图,运行相应的程序,则输出S的值为( )
阅读如图所示的框图,运行相应的程序,则输出S的值为( )
 阅读如图所示的框图,运行相应的程序,则输出S的值为( )
阅读如图所示的框图,运行相应的程序,则输出S的值为( )| A. | -1008 | B. | -1007 | C. | 1007 | D. | 1008 |