题目内容
设a为实常数，函数f（x）=-x3+ax2-4．
（1）若函数y=f（x）的图象在点P（1，f（1））处的切线的倾斜角为
，求函数f（x）的单调区间；
（2）若存在x0∈（0，+∞），使f（x0）＞0，求a的取值范围．
（1）若函数y=f（x）的图象在点P（1，f（1））处的切线的倾斜角为
| π |
| 4 |
（2）若存在x0∈（0，+∞），使f（x0）＞0，求a的取值范围．
（1）f′（x）=-3x2+2ax．根据题意f′（1）=tan
=1，
∴-3+2a=1，即a=2．∴f′（x）=-3x2+4x=-3x(x-
)．
当f′（x）＞0，得x(x-
)＜0，即0＜x＜
；当f′（x）＜0，得x(x-
)＞0，即x＜0或x＞
．
∴f′（x）的单调递增区间是(0，
)，单调递减区间是（-∞，0）∪(
，+∞)；
（2）f′（x）=-3x(x-
)．
①若a≤0，当x＞0时，f′（x）＜0，从而f（x）在（0，+∞）上是减函数，
又f（0）=-4，则当x＞0时，f（x）＜-4．
∴当a≤0时，不存在x0＞0，使f（x0）＞0；
②当a＞0，则当0＜x＜
时，f′（x）＞0，当x＞
时，f′（x）＜0．
从而f（x）在(0，
)上单调递增，在(
，+∞)上单调递减．
∴当x∈（0，+∞）时，f（x）max=f(
)=-
+
-4=
-4．
据题意，
-4＞0，即a3＞27，∴a＞3．
故a的取值范围是（3，+∞）．
| π |
| 4 |
∴-3+2a=1，即a=2．∴f′（x）=-3x2+4x=-3x(x-
| 4 |
| 3 |
当f′（x）＞0，得x(x-
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
∴f′（x）的单调递增区间是(0，
| 4 |
| 3 |
| 4 |
| 3 |
（2）f′（x）=-3x(x-
| 2a |
| 3 |
①若a≤0，当x＞0时，f′（x）＜0，从而f（x）在（0，+∞）上是减函数，
又f（0）=-4，则当x＞0时，f（x）＜-4．
∴当a≤0时，不存在x0＞0，使f（x0）＞0；
②当a＞0，则当0＜x＜
| 2a |
| 3 |
| 2a |
| 3 |
从而f（x）在(0，
| 2a |
| 3 |
| 2a |
| 3 |
∴当x∈（0，+∞）时，f（x）max=f(
| 2a |
| 3 |
| 8a3 |
| 27 |
| 4a3 |
| 9 |
| 4a3 |
| 27 |
据题意，
| 4a3 |
| 27 |
故a的取值范围是（3，+∞）．
练习册系列答案
相关题目
，求a的值；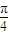
，求函数f（x）的单调区间；