Question

【题目】已知， .

（1）求函数的最小值；

（2）对一切， 恒成立，求实数的取值范围.

Answer 1

【答案】(1) ;(2) .

【解析】试题分析：（1）求出，利用导数与单调性的关系，分类求解；（2））由已知， ，分离参数，则，构造 (x＞0) 通过研究h（x）的最值确定a的范围．

试题解析：解：（1），

当， ，f(x)单调递减，当， ，f(x)单调递增

①，没有最小值；

②，即时， ；

③，即时，f（x）在[t，t+2]上单调递增， ；

所以;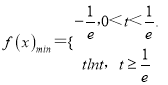

（2）由已知， ，则，

设，则，

①x∈（0，1），h'（x）＜0，h（x）单调递减，

②x∈（1，+∞），h'（x）＞0，h（x）单调递增，

所以h（x）min=h（1）=4，对一切x∈（0，+∞），2f（x）≥g（x）恒成立，

所以a≤h（x）min=4；，所以a的范围是（-∞，4].