题目内容
已知椭圆 的两个焦点分别是F1,F2,P是这个椭圆上的一个动点,延长F1P到Q,使得|PQ|=|F2P|,求Q的轨迹方程是________.
的两个焦点分别是F1,F2,P是这个椭圆上的一个动点,延长F1P到Q,使得|PQ|=|F2P|,求Q的轨迹方程是________.
(x+1)2+y2=16
分析:由题意可知,点Q的轨迹是以F1(-1,0)为圆心,以|F1Q|=4为半径的圆.由此可心求出其方程.
解答:∵F1(-1,0),F2(1,0),|PF1|+|PF2|=2a=4,
|PQ|=|F2P|,∴|F1Q|=|F1P|+|F2P|=2a=4,
∴Q的轨迹是以F1(-1,0)为圆心,以|F1Q|=4为半径的圆,
其方程为(x+1)2+y2=16.
答案:(x+1)2+y2=16.
点评:本题考查椭圆的性质和圆的方程,解题要注意审题,避免出错.
分析:由题意可知,点Q的轨迹是以F1(-1,0)为圆心,以|F1Q|=4为半径的圆.由此可心求出其方程.
解答:∵F1(-1,0),F2(1,0),|PF1|+|PF2|=2a=4,
|PQ|=|F2P|,∴|F1Q|=|F1P|+|F2P|=2a=4,
∴Q的轨迹是以F1(-1,0)为圆心,以|F1Q|=4为半径的圆,
其方程为(x+1)2+y2=16.
答案:(x+1)2+y2=16.
点评:本题考查椭圆的性质和圆的方程,解题要注意审题,避免出错.

练习册系列答案
相关题目
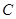 :
:
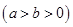 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 ,椭圆
,椭圆 满足
满足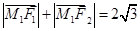 .
.
 作直线
作直线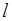 ,使得直线
,使得直线 .求出
.求出 的值.
的值. :
:
 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 ,椭圆
,椭圆 满足
满足 .
. (0,
(0,  )
) ,使得过点
,使得过点 与椭圆
与椭圆 .若存在,请求出
.若存在,请求出 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。 :
:
 ,称圆心在坐标原点
,称圆心在坐标原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 ,椭圆
,椭圆 满足
满足 .
.
 作直线
作直线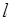 ,使得直线
,使得直线 .求出
.求出 的值.
的值.